Back to the topics list

wyrażenie algebraiczne

Zawartość:

• Co to jest zmienna?
• Rodzaje wyrażeń algebraicznych.
• Współczynnik.
• Warunki podobne i niepodobne.
• Wielomian.
• Dodawanie, odejmowanie, mnożenie i dzielenie wyrażeń algebraicznych.
• Zastosowanie zasady kolejności działań w celu uproszczenia wyrażeń algebraicznych.

Dosłowne liczby

W algebrze używamy alfabetu angielskiego lub greckiego, takiego jak a, b, x, y, β, Φ, ... do reprezentowania liczb. Te litery są używane do reprezentowania nieznanych ilości. Ponieważ litery reprezentują liczby, nazywa się je liczbami literalnymi. Dosłowna liczba może przyjąć dowolną wartość, dlatego nazywamy ją zmienną . Liczbę o określonej wartości nazywamy stałą.

Wyrażenie algebraiczne

Kombinacja stałych i literałów (zmiennych) połączonych przez jedną lub więcej operacji arytmetycznych (dodawanie, mnożenie, odejmowanie, dzielenie) nazywana jest wyrażeniem algebraicznym. Jeden lub więcej znaków (+, −) dzieli wyrażenie algebraiczne na kilka części. Każda część z jej znakiem nazywana jest wyrazem wyrażenia algebraicznego. Termin może być stałą, jak na przykład 4, zmienną, na przykład, x, iloczynem stałej i zmiennej, na przykład, 4x lub iloczynem dwóch lub więcej zmiennych, na przykład, xy, xy ² .

Jednomian: Wyrażenie algebraiczne, które ma tylko jeden wyraz, nazywane jest jednomianem. Przykład: 7x, ab ² , 8
Dwumian: Wyrażenie algebraiczne, które ma dwa wyrazy, nazywane jest dwumianem. Przykład: x ² + y ² , x + 2
Trójmian: Wyrażenie algebraiczne, które ma trzy wyrazy, nazywane jest trójmianem. Przykład: x ² + y ² + z ² , x + y +2

Współczynnik

Każda z wielkości (stała lub literały) pomnożona w celu utworzenia produktu nazywana jest czynnikiem produktu, a każdy czynnik w produkcie nazywany jest współczynnikiem iloczynu pozostałych czynników. W wyrazie -11p ² q wyrażenia 5p ³ − 11p ² q + 7,

• Współczynnik numeryczny wynosi -11.
• Dosłowny współczynnik to p ² q.
• Współczynnik p ² wynosi -11q.
• Współczynnik -11p ² wynosi q.
  

Warunki podobne i niepodobne

Mówi się, że wyrazy wyrażenia algebraicznego mające tę samą zmienną (zmienne) i ten sam wykładnik (wykładniki) zmiennych są podobne do wyrazów. Podobny termin może różnić się tylko współczynnikami.
2xy+ 3x + 4y + 5xy + 7y
Wyrazy 2xy i 5xy są wyrazami podobnymi. 4y i 7y są jak wyrazy.

Wszystkie wyrazy w wyrażeniu algebraicznym 2x + 3xy + 5y są różne.

Wielomian

Wyrażenie algebraiczne, w którym potęgi zaangażowanych zmiennych są nieujemnymi liczbami całkowitymi, nazywa się wielomianem.

\(x^3+ x^2 + 2x + 1\) jest wielomianem w jednej zmiennej x.
\(6x - \frac{4x}{y} + 2y + 3 \) nie jest wielomianem (zauważ, że y w drugim wyrazie ma potęgę -1)

Dodawanie i odejmowanie podobnych warunków

Aby połączyć podobne wyrazy przez dodawanie lub odejmowanie, po prostu dodaj lub odejmij współczynniki liczbowe podanych wyrazów.
Przykład:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Dodawanie i odejmowanie wyrażeń algebraicznych

Aby dodać wyrażenie algebraiczne, po prostu dodaj ich podobne warunki. Dla wygody napisz podobny termin jeden pod drugim w tej samej kolumnie. Przykład:
Dodać -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

W przypadku odejmowania odwróć znak każdego wyrazu odejmowanego wyrażenia, a następnie dodaj oba wyrażenia. Przykład
Odejmij \(3x^2 + 5x + 7y^2\) od \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Możesz także dodawać lub odejmować wyrażenia algebraiczne za pomocą Grupowania. Weźmy powyższy przykład i odejmijmy za pomocą Grupowania:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Mnożenie wyrażeń algebraicznych

Mnożenie wyrażeń algebraicznych można podzielić na trzy przypadki, omówmy je osobno:

Sprawa I (Mnożenie jednomianów) : Pomnóż ich współczynniki liczbowe, a następnie zmienne, dodając wykładniki wspólnych zmiennych, pozostawiając niezmienione zmienne rzadkie. Przykład: Znajdź iloczyn 6bc i 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Sprawa II (Mnożenie wielomianu przez jednomian) : Pomnóż każdy wyraz wielomianu przez jednomian. Przykład: Iloczyn 3xy i x ² + 2xy + y ² to
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Sprawa III (Mnożenie wielomianu przez wielomian) : Pomnóż każdy wyraz jednego wielomianu przez każdy wyraz drugiego, a następnie połącz podobne wyrazy, aby uprościć iloczyn. Przykład: Iloczyn (2x + 3y) i ( x + y + 2) to
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Podział wyrażeń algebraicznych

Podział wyrażeń algebraicznych można wyjaśnić za pomocą trzech poniższych przypadków.

Sprawa I (Dzielenie jednomianu przez jednomian) : Aby podzielić jednomian przez jednomian, znajdź iloraz ich współczynników liczbowych i iloraz zmiennych, odejmując wykładniki wspólnych zmiennych. Przykład:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Sprawa II (Dzielenie wielomianu przez jednomian) : Podziel każdy wyraz wielomianu przez jednomian, a następnie podziel tak, jak podano w powyższym przypadku. Przykład:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Sprawa III ( Dzielenie wielomianu przez wielomian ): Zostanie to wykonane metodą długiego dzielenia. Spróbujmy to zrozumieć na przykładzie.
\(8x^2 + 9x - 8 \div 8x + 1\)

Rozpocznij od podzielenia pierwszego wyrazu dzielnej (8x ² ) przez pierwszy wyraz dzielnika (8x), aby znaleźć pierwszy wyraz ilorazu (x), a następnie pomnóż iloraz przez dzielnik i odejmij.

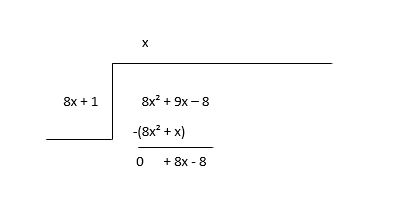
Rozważ resztę jako nową dywidendę i oszacuj następny wyraz ilorazu.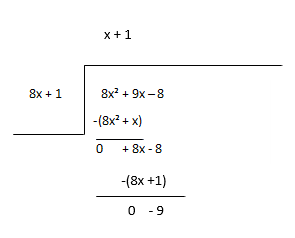

Iloraz - x + 1, reszta - -9

Usunięcie nawiasów i użycie reguły kolejności operacji

Aby uprościć wyrażenie algebraiczne zawierające nawiasy, usuń nawiasy w kolejności:

Przykład:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)