Back to the topics list

expressão algébrica

Conteúdo:

• O que é uma Variável?
• Tipos de Expressão Algébrica.
• Coeficiente.
• Termos de gostar e não gostar.
• Polinomial.
• Adição, subtração, multiplicação e divisão de expressão algébrica.
• Aplicação da regra de ordem de operações para simplificar a expressão algébrica.

Números Literais

Em álgebra usamos alfabetos ingleses ou gregos como a, b, x, y, β, Φ, ... para representar números. Essas letras são usadas para representar quantidades desconhecidas. Como as letras representam números, elas são chamadas de números literais. Um número literal pode assumir qualquer valor, por isso o chamamos de variável . Um número com um valor definido é chamado de constante.

Expressão algébrica

Uma combinação de constantes e literais (variáveis) conectadas por uma ou mais operações aritméticas (adição, multiplicação, subtração, divisão) é chamada de expressão algébrica. Um ou mais sinais (+, −) dividem uma expressão algébrica em várias partes. Cada parte com seu sinal é chamada de termo da expressão algébrica. Um termo pode ser uma constante como, por exemplo, 4, uma variável, por exemplo, x, um produto de uma constante e uma variável, por exemplo, 4x ou um produto de duas ou mais variáveis, por exemplo, xy, xy ² .

Monômio: Uma expressão algébrica que tem apenas um termo é chamada de monômio. Exemplo: 7x, ab ² , 8
Binomial: Uma expressão algébrica que tem dois termos é chamada de binomial. Exemplo: x ² + y ² , x + 2
Trinômio: Uma expressão algébrica que possui três termos é chamada de trinômio. Exemplo: x ² + y ² + z ² , x + y +2

Coeficiente

Cada uma das quantidades (constantes ou literais) multiplicadas para formar um produto é chamada de fator do produto e qualquer fator em um produto é chamado de coeficiente do produto dos fatores restantes. No termo, -11p ² q da expressão 5p ³ − 11p ² q + 7,

• O coeficiente numérico é -11.
• O coeficiente literal é p ² q.
• O coeficiente de p ² é -11q.
• O coeficiente de -11p ² é q.
  

Termos de gostar e não gostar

Os termos da expressão algébrica tendo a(s) mesma(s) variável(is) e o(s) mesmo(s) expoente(s) das variáveis são chamados de termos semelhantes. O mesmo termo pode diferir apenas em coeficientes.
2xy + 3x + 4y + 5xy + 7y
Os termos 2xy e 5xy são termos semelhantes. 4y e 7y são termos semelhantes.

Os termos na expressão algébrica 2x + 3xy + 5y são todos diferentes.

Polinomial

Uma expressão algébrica na qual as potências das variáveis envolvidas são inteiros não negativos é chamada de polinômio.

\(x^3+ x^2 + 2x + 1\) é um polinômio em uma variável x.
\(6x - \frac{4x}{y} + 2y + 3 \) não é um polinômio (observe que y no segundo termo tem potência -1)

Adição e subtração de termos semelhantes

Para combinar termos semelhantes por adição ou subtração, basta somar ou subtrair os coeficientes numéricos dos termos dados.
Exemplo:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Adição e Subtração de Expressões Algébricas

Para adicionar expressões algébricas, simplesmente adicione seus termos semelhantes. Por conveniência, escreva o termo semelhante um abaixo do outro na mesma coluna. Exemplo:
Adicionar -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Para subtração , inverta o sinal de cada termo da expressão que está sendo subtraída e, em seguida, some as duas expressões juntas. Exemplo
Subtraia \(3x^2 + 5x + 7y^2\) de \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Você também pode adicionar ou subtrair expressões algébricas usando Agrupamento. Vamos pegar o exemplo acima e subtrair usando Agrupamento:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Multiplicação de Expressões Algébricas

A multiplicação da expressão algébrica pode ser dividida em três casos, vamos discuti-los separadamente:

Caso EU (Multiplicação de monômios) : Multiplique seus coeficientes numéricos juntos e depois as variáveis somando os expoentes das variáveis comuns, deixando as variáveis incomuns inalteradas. Exemplo: Encontre o produto de 6bc e 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Caso II (Multiplicação polinomial por um monômio) : Multiplique cada termo do polinômio pelo monômio. Exemplo: O produto de 3xy e x ² + 2xy + y ² é
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Caso III (Multiplicação de um polinômio por polinômio) : Multiplique cada termo de um polinômio por todos os termos do outro e depois combine os termos semelhantes para simplificar o produto. Exemplo: Produto de (2x + 3y) e ( x + y + 2) é
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Divisão de Expressões Algébricas

A divisão da expressão algébrica pode ser explicada usando três casos abaixo.

Caso EU (Divisão de um monômio por um monômio) : Para dividir um monômio por um monômio, encontre os quocientes de seus coeficientes numéricos e os quocientes das variáveis subtraindo os expoentes de variáveis comuns.Exemplo:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Caso II (Divisão de Polinômio por Monômio) : Divida cada termo do polinômio por um monômio e então divida como dado no caso acima.Exemplo:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Caso III ( Divisão de um polinômio por um polinômio ): Isso será feito pelo método da divisão longa. Vamos tentar entender isso usando um exemplo.
\(8x^2 + 9x - 8 \div 8x + 1\)

Comece dividindo o primeiro termo do dividendo (8x ² ) pelo primeiro termo do divisor (8x) para encontrar o primeiro termo do quociente (x) e, em seguida, multiplique o quociente pelo divisor e subtraia.

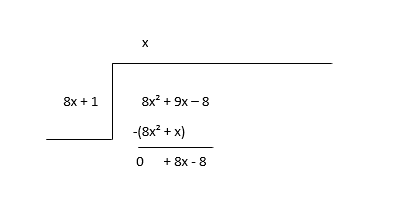
Considere o restante como o novo dividendo e estime o próximo termo do quociente.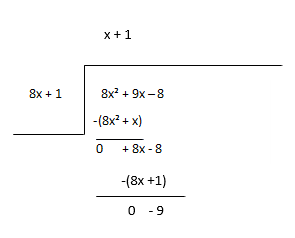

Quociente - x + 1, Resto - -9

Remoção de colchetes e uso da regra de ordem de operações

Para simplificar uma expressão algébrica contendo colchetes, remova os colchetes na ordem de:

Exemplo:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)