Back to the topics list

алгебраическое выражение

Содержание:

• Что такое переменная?
• Типы алгебраических выражений.
• Коэффициент.
• Как и в отличие от терминов.
• Полиномиальный.
• Сложение, вычитание, умножение и деление алгебраического выражения.
• Применение правила порядка операций для упрощения алгебраического выражения.

Буквенные числа

В алгебре мы используем английский или греческий алфавиты, такие как a, b, x, y, β, Φ, ... для представления чисел. Эти буквы используются для обозначения неизвестных величин. Поскольку буквы обозначают числа, их называют буквальными числами. Буквенное число может принимать любое значение, поэтому мы называем его переменной . Число с определенным значением называется константой.

Алгебраическое выражение

Комбинация констант и литералов (переменных), связанных одной или несколькими арифметическими операциями (сложение, умножение, вычитание, деление), называется алгебраическим выражением. Один или несколько знаков (+, −) разбивают алгебраическое выражение на несколько частей. Каждая часть со своим знаком называется членом алгебраического выражения. Терм может быть константой, например, 4, переменной, например, x, произведением константы и переменной, например, 4x или произведением двух или более переменных, например, xy, xy ² .

Моном: алгебраическое выражение, которое имеет только один член, называется мономом. Пример: 7x, аб ² , 8
Биномиальное: алгебраическое выражение, состоящее из двух членов, называется биномиальным. Пример: х ² + у ² , х + 2
Трехчлен: алгебраическое выражение, состоящее из трех членов, называется трехчленом. Пример: х ² + у ² + z ² , х + у +2

Коэффициент

Каждая из величин (постоянных или литералов), умноженных для образования продукта, называется фактором продукта, а любой фактор продукта называется коэффициентом произведения остальных факторов. В члене -11p ² q выражения 5p ³ − 11p ² q + 7,

• Числовой коэффициент равен -11.
• Буквенный коэффициент равен p ² q.
• Коэффициент p ² равен -11q.
• Коэффициент -11p ² равен q.
  

Нравятся и не нравятся термины

Термины алгебраического выражения, имеющие одну и ту же переменную (переменные) и один и тот же показатель (ы) переменных, называются подобными терминам. Подобный член может отличаться только коэффициентами.
2xy+ 3x + 4y + 5xy + 7y
Термины 2xy и 5xy подобны терминам. 4y и 7y подобны терминам.

Члены алгебраического выражения 2x + 3xy + 5y не похожи друг на друга.

Полиномиальный

Алгебраическое выражение, в котором степени участвующих переменных являются целыми неотрицательными числами, называется полиномом.

\(x^3+ x^2 + 2x + 1\) — многочлен от одной переменной x.
\(6x - \frac{4x}{y} + 2y + 3 \) не является многочленом (обратите внимание, что y во втором члене имеет степень -1)

Добавление и вычитание подобных терминов

Чтобы объединить одинаковые термины путем сложения или вычитания, просто добавьте или вычтите числовые коэффициенты данных терминов.
Пример:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Сложение и вычитание алгебраических выражений

Чтобы добавить алгебраическое выражение, просто добавьте их похожие термины. Для удобства записывайте одинаковые термины один под другим в том же столбце. Пример:
Добавлять -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Для вычитания переверните знак каждого члена вычитаемого выражения, а затем сложите два выражения вместе. Пример
Вычтите \(3x^2 + 5x + 7y^2\) из \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Вы также можете добавлять или вычитать алгебраические выражения с помощью группировки. Давайте возьмем приведенный выше пример и вычтем с помощью группировки:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Умножение алгебраических выражений

Умножение алгебраического выражения можно разделить на три случая, давайте обсудим их отдельно:

Случай я (Умножение мономов) : умножьте их числовые коэффициенты вместе, а затем переменные, добавив показатели общих переменных, оставив необычные переменные без изменений. Пример: Найдите произведение 6bc и 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Случай II (Умножение многочлена на моном) : Умножьте каждый член многочлена на одночлен. Пример: Произведение 3xy и x ² + 2xy + y ² равно
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Случай III (Умножение многочлена на многочлен) : умножьте каждый член одного многочлена на каждый член другого, а затем объедините одинаковые члены, чтобы упростить произведение. Пример: Произведение (2x + 3y) и (x + y + 2) равно
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Отдел алгебраических выражений

Разделение алгебраического выражения можно объяснить с помощью следующих трех случаев.

Случай я (Деление монома на моном) : Чтобы разделить моном на моном, найдите отношения их числовых коэффициентов и отношения переменных путем вычитания показателей общих переменных. Пример:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Случай II (Деление многочлена на моном) : разделите каждый член многочлена на одночлен, а затем разделите, как указано в приведенном выше случае. Пример:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Случай III ( Деление многочлена на многочлен ): это будет сделано методом длинного деления. Попробуем понять это на примере.
\(8x^2 + 9x - 8 \div 8x + 1\)

Начните с деления первого члена делимого (8x ² ) на первый член делителя (8x), чтобы найти первый член частного (x), а затем умножьте частное члена на делитель и вычтите.

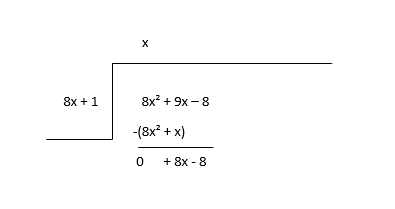
Считайте остаток новым делимым и оцените следующий член частного.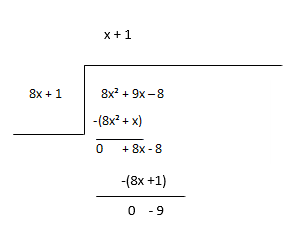

Частное - х + 1, остаток - -9

Снятие скобок и использование правила порядка операций

Чтобы упростить алгебраическое выражение, содержащее скобки, удалите скобки в следующем порядке:

Пример:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)