Back to the topics list

shprehje algjebrike

Përmbajtja:

• Çfarë është një variabël?
• Llojet e shprehjeve algjebrike.
• Koeficient.
• Kushtet e pëlqimit dhe ndryshimit.
• Polinom.
• Mbledhja, zbritja, shumëzimi dhe pjesëtimi i shprehjes algjebrike.
• Zbatimi i rregullit të rendit të veprimeve për të thjeshtuar shprehjen algjebrike.

Numrat Literal

Në Algjebër ne përdorim alfabete angleze ose greke si a, b, x, y, β, Φ, ... për të paraqitur numrat. Këto shkronja përdoren për të përfaqësuar sasi të panjohura. Meqenëse shkronjat përfaqësojnë numra, ato quhen numra të drejtpërdrejtë. Një numër literal mund të marrë çdo vlerë, prandaj ne e quajmë atë një ndryshore . Një numër me një vlerë të caktuar quhet konstante.

Shprehje Algjebrike

Një kombinim i konstanteve dhe literaleve (ndryshoreve) të lidhura me një ose më shumë veprime aritmetike (mbledhje, shumëzim, zbritje, pjesëtim) quhet shprehje algjebrike. Një ose më shumë shenja (+, −) ndajnë një shprehje algjebrike në disa pjesë. Çdo pjesë me shenjën e saj quhet term i shprehjes algjebrike. Një term mund të jetë një konstante si për shembull 4, një ndryshore, për shembull, x, një produkt i një konstante dhe ndryshoreje, për shembull, 4x ose një produkt i dy ose më shumë ndryshoreve, për shembull, xy, xy ² .

Monomi: Një shprehje algjebrike që ka vetëm një term quhet monom. Shembull: 7x, ab ² , 8
Binom: Një shprehje algjebrike që ka dy terma quhet binom. Shembull: x ² + y ² , x + 2
Trinomi: Një shprehje algjebrike që ka tre terma quhet trinom. Shembull: x ² + y ² + z ² , x +y +2

Koeficient

Secila nga sasitë (konstante ose literale) e shumëzuar për të formuar një produkt, quhet faktor i produktit dhe çdo faktor në një produkt quhet koeficienti i prodhimit të faktorëve të mbetur. Në termin, -11p ² q të shprehjes 5p ³ − 11p ² q + 7,

• Koeficienti numerik është -11.
• Koeficienti literal është p ² q.
• Koeficienti i p ² është -11q.
• Koeficienti -11p ² është q.
  

Kushtet e pëlqimit dhe ndryshimit

Termat e shprehjes algjebrike që kanë të njëjtat ndryshore dhe eksponentë të njëjtë të variablave thuhet se janë si terma. Termi i ngjashëm mund të ndryshojë vetëm në koeficientë.
2xy+ 3x + 4y + 5xy + 7y
Termat 2xy dhe 5xy janë si terma. 4v dhe 7v janë si terma.

Termat në shprehjen algjebrike 2x + 3xy + 5y janë të gjithë të ndryshëm.

Polinom

Një shprehje algjebrike në të cilën fuqitë e ndryshoreve të përfshira janë numra të plotë jo-negativë quhet polinom.

\(x^3+ x^2 + 2x + 1\) është një polinom në një ndryshore x.
\(6x - \frac{4x}{y} + 2y + 3 \) nuk është një polinom (vini re se y në termin e dytë ka fuqi -1)

Mbledhja dhe zbritja e termave të ngjashëm

Për të kombinuar terma të ngjashëm me mbledhje ose zbritje, thjesht shtoni ose zbritni koeficientët numerikë të termave të dhënë.
Shembull:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Mbledhja dhe zbritja e shprehjeve algjebrike

Për të shtuar shprehje algjebrike, thjesht shtoni termat e tyre si. Për lehtësi, shkruani termin e ngjashëm njëri nën tjetrin në të njëjtën kolonë. Shembull:
Shto -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Për zbritje , ktheni shenjën e secilit term të shprehjes që po zbritet dhe më pas mblidhni dy shprehjet së bashku. Shembull
Zbrisni \(3x^2 + 5x + 7y^2\) nga \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Ju gjithashtu mund të shtoni ose zbrisni shprehje algjebrike duke përdorur Grupimin. Le të marrim shembullin e mësipërm dhe të zbresim duke përdorur Grupimin:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Shumëzimi i shprehjeve algjebrike

Shumëzimi i shprehjes algjebrike mund të ndahet në tre raste, le t'i diskutojmë ato veçmas:

Rast I (Shumëzimi i monomeve) : Shumëzoni së bashku koeficientët e tyre numerikë dhe më pas variablat duke shtuar eksponentët e ndryshoreve të zakonshme, duke i lënë të pandryshuara ndryshoret e pazakonta. Shembull: Gjeni prodhimin e 6bc dhe 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Rast II (Polinomi i shumëzimit me një monom) : Shumëzoni çdo term të polinomit me monomin. Shembull: Produkti i 3xy dhe x ² + 2xy + y ² është
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Rast III (Shumëzimi i një polinomi me polinom) : Shumëzoni çdo term të një polinomi me çdo term të tjetrit dhe më pas kombinoni termat e ngjashëm për të thjeshtuar produktin. Shembull: Produkti i (2x + 3y) dhe (x + y + 2) është
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Ndarja e shprehjeve algjebrike

Ndarja e shprehjes algjebrike mund të shpjegohet duke përdorur më poshtë tre raste.

Rast I (Pjestimi i një monomi me një monom) : Për të pjesëtuar një monom me një monom, gjeni herësin e koeficientëve të tyre numerikë dhe herësit e ndryshoreve duke zbritur eksponentët e ndryshoreve të zakonshme. Shembull:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Rast II (Pjestimi i polinomit me monom) : Ndani çdo term të polinomit me një monom dhe më pas pjesëtoni siç është dhënë në rastin e mësipërm. Shembull:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Rast III ( Pjestimi i një polinomi me një polinom ): Kjo do të bëhet me metodën e ndarjes së gjatë. Le të përpiqemi ta kuptojmë këtë duke përdorur një shembull.
\(8x^2 + 9x - 8 \div 8x + 1\)

Filloni duke pjesëtuar termin e parë të dividendit (8x ² ) me anëtarin e parë të pjesëtuesit (8x) për të gjetur termin e parë të herësit (x) dhe më pas shumëzoni termin herës me pjesëtuesin dhe zbrisni.

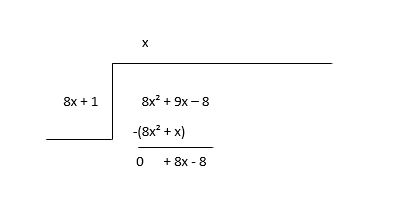
Konsideroni pjesën e mbetur si divident të ri dhe vlerësoni termin tjetër të koeficientit.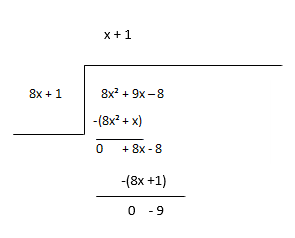

Koeficienti - x + 1, pjesa e mbetur - -9

Heqja e kllapave dhe përdorimi i Rregullës së Rendit të Operacioneve

Për të thjeshtuar një shprehje algjebrike që përmban kllapa, hiqni kllapat në rendin e:

Shembull:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)