Back to the topics list

algebraiska uttryck

Innehåll:

• Vad är en variabel?
• Typer av algebraiska uttryck.
• Koefficient.
• Villkor för gilla och olik.
• Polynom.
• Addition, subtraktion, multiplikation och division av algebraiska uttryck.
• Tillämpning av Order of Operations-regeln för att förenkla algebraiskt uttryck.

Bokstavliga siffror

I algebra använder vi engelska eller grekiska alfabet som a, b, x, y, β, Φ, ... för att representera tal. Dessa bokstäver används för att representera okända kvantiteter. Eftersom bokstäver representerar siffror så kallas de bokstavliga siffror. Ett bokstavligt tal kan anta vilket värde som helst, därför kallar vi det en variabel . Ett tal med ett bestämt värde kallas en konstant.

Algebraiska uttryck

En kombination av konstanter och literaler (variabler) sammankopplade med en eller flera aritmetiska operationer (addition, multiplikation, subtraktion, division) kallas ett algebraiskt uttryck. Ett eller flera tecken (+, −) delar upp ett algebraiskt uttryck i flera delar. Varje del med sitt tecken kallas en term för det algebraiska uttrycket. En term kan vara en konstant som till exempel 4, en variabel, till exempel x, en produkt av en konstant och variabel, till exempel 4x eller en produkt av två eller flera variabler, till exempel xy, xy ² .

Monomial: Ett algebraiskt uttryck som bara har en term kallas monomial. Exempel: 7x, ab ² , 8
Binomial: Ett algebraiskt uttryck som har två termer kallas binomial. Exempel: x ² + y ² , x + 2
Trinomial: Ett algebraiskt uttryck som har tre termer kallas trinomial. Exempel: x ² + y ² + z ² , x + y +2

Koefficient

Var och en av kvantiteterna (konstanta eller bokstavliga) multiplicerade för att bilda en produkt, kallas en faktor för produkten och varje faktor i en produkt kallas koefficienten för produkten av de återstående faktorerna. I termen -11p ² q av uttrycket 5p ³ − 11p ² q + 7,

• Numerisk koefficient är -11.
• Den bokstavliga koefficienten är p ² q.
• Koefficienten för p ² är -11q.
• Koefficienten -11p ² är q.
  

Villkor för gilla och olik

Termerna för det algebraiska uttrycket som har samma variabel(er) och samma exponent(er) för variablerna sägs vara lika termer. Liknande term kan endast skilja sig i koefficienter.
2xy+ 3x + 4y + 5xy + 7y
Termerna 2xy och 5xy är liknande termer. 4y och 7y är liknande termer.

Termer i det algebraiska uttrycket 2x + 3xy + 5y är alla olika.

Polynom

Ett algebraiskt uttryck där potenserna för de inblandade variablerna är icke-negativa heltal kallas ett polynom.

\(x^3+ x^2 + 2x + 1\) är ett polynom i en variabel x.
\(6x - \frac{4x}{y} + 2y + 3 \) är inte ett polynom (lägg märke till att y i den andra termen har potens -1)

Tillägg och subtraktion av liknande villkor

För att kombinera liknande termer genom addition eller subtraktion, addera eller subtrahera helt enkelt de numeriska koefficienterna för de givna termerna.
Exempel:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Addition och subtraktion av algebraiska uttryck

För att lägga till algebraiska uttryck, lägg helt enkelt till deras liknande termer. För enkelhets skull skriv liknande term under varandra i samma kolumn. Exempel:
Lägg till -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

För subtraktion vänder du på tecknet för varje term i uttrycket som subtraheras och lägger sedan ihop de två uttrycken. Exempel
Subtrahera \(3x^2 + 5x + 7y^2\) från \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Du kan också lägga till eller subtrahera algebraiska uttryck med hjälp av gruppering. Låt oss ta exemplet ovan och subtrahera med hjälp av gruppering:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Multiplikation av algebraiska uttryck

Multiplikation av algebraiskt uttryck kan delas in i tre fall, låt oss diskutera dem separat:

Fall jag (Multiplicering av monomer) : Multiplicera deras numeriska koefficienter tillsammans och sedan variablerna genom att lägga till exponenterna för vanliga variabler, lämna de ovanliga variablerna oförändrade. Exempel: Hitta produkten av 6bc och 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Fall II (Multiplikationspolynom med ett mononom) : Multiplicera varje term i polynomet med monomet. Exempel: Produkt av 3xy och x ² + 2xy + y ² är
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Fall III (Multiplikation av ett polynom med polynom) : Multiplicera varje term i ett polynom med varje term i den andra och kombinera sedan liknande termer för att förenkla produkten. Exempel: Produkt av (2x + 3y) och ( x + y + 2) är
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Uppdelning av algebraiska uttryck

Division av algebraiskt uttryck kan förklaras med hjälp av nedanstående tre fall.

Fall jag (Division av en monomial med en monomial) : För att dividera en monomial med en monomial, hitta kvoterna för deras numeriska koefficienter och kvoterna för variablerna genom att subtrahera exponenterna för vanliga variabler.Exempel:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Fall II (Division av polynom med monomer) : Dividera varje term i polynomet med ett monom och dividera sedan enligt ovanstående fall.Exempel:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Fall III ( Division av ett polynom med ett polynom ): Detta kommer att göras med den långa divisionsmetoden. Låt oss försöka förstå detta med hjälp av ett exempel.
\(8x^2 + 9x - 8 \div 8x + 1\)

Börja med att dividera den första termen av utdelningen(8x ² ) med den första termen av divisorn(8x) för att hitta den första termen av kvoten(x) och sedan multiplicerar du kvottermen med divisorn och subtraherar.

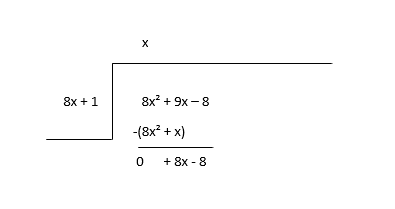
Betrakta resten som den nya utdelningen och uppskatta nästa period av kvoten.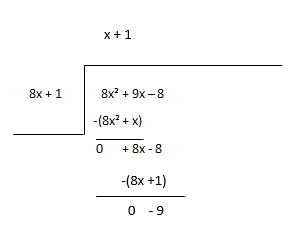

Kvotient - x + 1, Resterande - -9

Borttagning av parenteser och användning av Order of Operations-regeln

För att förenkla ett algebraiskt uttryck som innehåller parenteser tar du bort parenteserna i ordningen:

Exempel:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)