Back to the topics list

kujieleza algebraic

Yaliyomo:

• Tofauti ni nini?
• Aina za Maonyesho ya Algebraic.
• Mgawo.
• Masharti ya Kupenda na Tofauti.
• Polynomial.
• Kuongeza, Kutoa, Kuzidisha na Mgawanyiko wa usemi wa Aljebra.
• Utumiaji wa sheria ya Utaratibu wa Uendeshaji ili kurahisisha usemi wa Aljebra.

Nambari halisi

Katika Aljebra tunatumia Alfabeti za Kiingereza au Kigiriki kama vile a, b, x, y, β, Φ, ... kuwakilisha nambari. Barua hizi hutumiwa kuwakilisha idadi isiyojulikana. Kwa kuwa herufi huwakilisha nambari kwa hivyo huitwa nambari halisi. Nambari halisi inaweza kuchukua thamani yoyote kwa hivyo tunaiita variable . Nambari yenye thamani ya uhakika inaitwa mara kwa mara.

Usemi wa Aljebra

Mchanganyiko wa viunzi na herufi(vigeu) vilivyounganishwa na oparesheni moja au zaidi za hesabu (kuongeza, kuzidisha, kutoa, kugawanya) huitwa usemi wa Aljebra. Ishara moja au zaidi (+, -) hugawanya usemi wa aljebra katika sehemu kadhaa. Kila sehemu yenye ishara yake inaitwa neno la usemi wa aljebra. Neno linaweza kuwa sawa kwa mfano 4, kutofautisha, kwa mfano, x, bidhaa ya kubadilika na kubadilika, kwa mfano, 4x au bidhaa ya vigeu viwili au zaidi, kwa mfano, xy, xy ² .

Monomia: usemi wa aljebra ambao una neno moja tu huitwa monomial. Mfano: 7x, ab ² , 8
Binomia: usemi wa aljebra ambao una istilahi mbili huitwa binomial. Mfano: x ² + y ² , x + 2
Utatu: Usemi wa aljebra ambao una istilahi tatu huitwa trinomial. Mfano: x ² + y ² + z ² , x +y +2

Mgawo

Kila moja ya kiasi (mara kwa mara au halisi) kinachozidishwa ili kuunda bidhaa, inaitwa kipengele cha bidhaa na kipengele chochote katika bidhaa kinaitwa mgawo wa bidhaa wa vipengele vilivyobaki. Katika neno -11p 2q ya usemi 5p ³ - ^{11p 2 q} + 7,

• Mgawo wa nambari ni -11.
• Mgawo halisi ni p ² q.
• Mgawo wa p ² ni -11q.
• Mgawo wa -11p ² ni q.
  

Masharti ya Kupenda na Tofauti

Masharti ya usemi wa aljebra kuwa na viwezo sawa na vielelezo sawa vya viambajengo vinasemekana kuwa kama istilahi. Neno kama vile linaweza kutofautiana katika coefficients pekee.
2xy+ 3x + 4y + 5xy + 7y
Masharti 2xy na 5xy ni kama istilahi. 4y na 7y ni kama masharti.

Masharti katika usemi wa aljebra 2x + 3xy + 5y yote hayafanani.

Polynomial

Usemi wa aljebra ambapo nguvu za vigeu vinavyohusika ni nambari kamili zisizo hasi huitwa polynomial.

\(x^3+ x^2 + 2x + 1\) ni neno la polynomia katika kigezo kimoja x.
\(6x - \frac{4x}{y} + 2y + 3 \) si polynomial (kumbuka kuwa y katika muhula wa pili ana nguvu -1)

Kuongeza na Kutoa Masharti Kama

Ili kuchanganya maneno kama hayo kwa kuongeza au kutoa, ongeza tu au uondoe mgawo wa nambari wa masharti uliyopewa.
Mfano:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Kuongeza na Kutoa Maneno ya Aljebra

Ili kuongeza usemi wa aljebra, ongeza tu yao kama maneno. Kwa urahisi wa kuandika neno kama hilo moja chini ya lingine kwenye safu wima sawa. Mfano:
Ongeza -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Kwa kutoa , pindua ishara ya kila neno la usemi unaotolewa na kisha ujumuishe vielezi hivyo viwili pamoja. Mfano
Ondoa \(3x^2 + 5x + 7y^2\) kutoka \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Unaweza pia kuongeza au kupunguza misemo ya aljebra kwa kutumia Kupanga. Wacha tuchukue mfano ulio hapo juu na uondoe kwa kutumia Kundi:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Kuzidisha Semi za Aljebra

Kuzidisha kwa usemi wa algebra inaweza kugawanywa katika kesi tatu, wacha tuzijadili kando:

Kesi I (Multiplication of Monomials) : Zidisha viambajengo vyao vya nambari pamoja na kisha viambajengo kwa kuongeza viambajengo vya viambajengo vya kawaida, ukiacha viambajengo visivyo vya kawaida bila kubadilika. Mfano: Tafuta bidhaa ya 6bc na 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Kesi II (Multiplication Polynomial by Monomial) : Zidisha kila neno la polynomial kwa monomial. Mfano: Bidhaa ya 3xy na x ² + 2xy + y ² ni
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Kesi III (Kuzidisha kwa Polynomial kwa Polynomial) : Zidisha kila neno la polynomia moja kwa kila neno la nyingine na kisha unganisha maneno kama hayo ili kurahisisha bidhaa. Mfano: Bidhaa ya (2x + 3y) na (x + y + 2) ni
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Sehemu ya Maneno ya Aljebra

Mgawanyiko wa usemi wa aljebra unaweza kuelezewa kwa kutumia visa vitatu hapa chini.

Kesi I (Mgawanyiko wa Monomia kwa Monomia) : Ili kugawanya monomia kwa monomia, tafuta nukuu za mgawo wao wa nambari na nukuu za vigeu kwa kutoa vipeo vya viambajengo vya kawaida.Mfano:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Kesi II (Mgawanyiko wa Polynomial kwa Monomial) : Gawanya kila neno la polynomial kwa monomia na kisha ugawanye kama ilivyotolewa katika hali iliyo hapo juu.Mfano:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Kesi III ( Division of a Polynomial by Polynomial ): Hii itafanywa kwa njia ya mgawanyiko mrefu. Hebu jaribu kuelewa hili kwa kutumia mfano.
\(8x^2 + 9x - 8 \div 8x + 1\)

Anza kwa kugawanya muhula wa kwanza wa mgao(8x ² ) na muhula wa kwanza wa kigawanyo(8x) ili kupata muhula wa kwanza wa mgawo(x) kisha unazidisha neno la mgawo na kigawanyaji na kutoa.

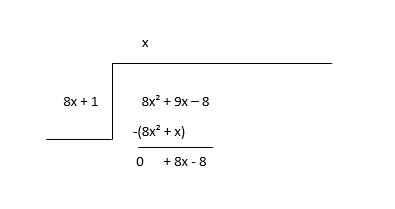
Zingatia salio kama mgao mpya na ukadiria muhula unaofuata wa mgawo huo.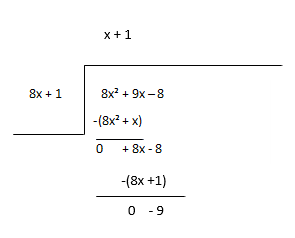

Nukuu - x + 1, Salio - -9

Uondoaji wa Mabano na matumizi ya Amri ya Sheria ya Uendeshaji

Ili kurahisisha usemi wa aljebra ulio na mabano, ondoa mabano kwa mpangilio wa :

Mfano:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)