Back to the topics list

นิพจน์พีชคณิต

เนื้อหา:

• ตัวแปรคืออะไร?
• ประเภทของนิพจน์พีชคณิต
• ค่าสัมประสิทธิ์
• เงื่อนไขการถูกใจและไม่ชอบ
• พหุนาม.
• การบวก ลบ คูณ หาร การแสดงออกทางพีชคณิต
• การประยุกต์ใช้กฎลำดับการดำเนินการเพื่อลดความซับซ้อนของนิพจน์พีชคณิต

ตัวเลขตัวอักษร

ในพีชคณิต เราใช้ตัวอักษรภาษาอังกฤษหรือกรีก เช่น a, b, x, y, β, Φ, ... เพื่อแสดงตัวเลข ตัวอักษรเหล่านี้ใช้แทนปริมาณที่ไม่รู้จัก เนื่องจากตัวอักษรแทนตัวเลขจึงเรียกว่าตัวเลขตามตัวอักษร จำนวนตามตัวอักษรสามารถรับค่าใดๆ ก็ได้ เราจึงเรียกว่า ตัวแปร จำนวนที่มีค่าแน่นอนเรียกว่า ค่าคงที่

นิพจน์เกี่ยวกับพีชคณิต

การรวมกันของค่าคงที่และตัวอักษร (ตัวแปร) ที่เชื่อมต่อกันด้วยการดำเนินการทางคณิตศาสตร์อย่างน้อยหนึ่งรายการ (การบวก การคูณ การลบ การหาร) เรียกว่านิพจน์เกี่ยวกับพีชคณิต เครื่องหมายอย่างน้อยหนึ่งเครื่องหมาย (+, -) แบ่งการแสดงออกทางพีชคณิตออกเป็นหลายส่วน แต่ละส่วนที่มีสัญลักษณ์เรียกว่า พจน์ ของนิพจน์พีชคณิต คำสามารถเป็นค่าคงที่ เช่น 4, ตัวแปร เช่น x, ผลคูณของค่าคงที่และตัวแปร เช่น 4x หรือผลคูณของตัวแปรสองตัวขึ้นไป เช่น xy, xy ²

Monomial: นิพจน์เกี่ยวกับพีชคณิตที่มีเพียงคำเดียวเรียกว่า monomial ตัวอย่าง: 7x, ab ² , 8
ทวินาม: นิพจน์เกี่ยวกับพีชคณิตที่มีสองคำเรียกว่าทวินาม ตัวอย่าง: x ² + y ² , x + 2
Trinomial: นิพจน์เกี่ยวกับพีชคณิตที่มีสามคำเรียกว่า trinomial ตัวอย่าง: x ² + y ² + z ² , x +y +2

ค่าสัมประสิทธิ์

แต่ละปริมาณ (ค่าคงที่หรือตัวอักษร) คูณกันเพื่อสร้างผลิตภัณฑ์ เรียกว่าตัวประกอบของผลิตภัณฑ์ และตัวประกอบใดๆ ในผลิตภัณฑ์เรียกว่าค่าสัมประสิทธิ์ของผลิตภัณฑ์ตัวประกอบที่เหลือ ในเทอม -11p ² q ของนิพจน์ 5p ³ − 11p ² q + 7

• ค่าสัมประสิทธิ์ตัวเลขคือ -11
• ค่าสัมประสิทธิ์ตามตัวอักษรคือ p ² q
• ค่าสัมประสิทธิ์ของ p ² คือ -11q
• ค่าสัมประสิทธิ์ของ -11p ² คือ q
  

เงื่อนไขการถูกใจและไม่ชอบ

พจน์ของนิพจน์พีชคณิตที่มีตัวแปรและเลขชี้กำลังของตัวแปรเหมือนกันจะกล่าวได้ว่าเหมือนกับพจน์ คำที่เหมือนกันอาจแตกต่างกันในค่าสัมประสิทธิ์เท่านั้น
2xy+ 3x + 4y + 5xy + 7y
เงื่อนไข 2xy และ 5xy เป็นเหมือนเงื่อนไข 4y และ 7y เป็นเหมือนเทอม

เงื่อนไขในนิพจน์พีชคณิต 2x + 3xy + 5y ไม่เหมือนกันทั้งหมด

พหุนาม

นิพจน์เกี่ยวกับพีชคณิตซึ่งกำลังของตัวแปรที่เกี่ยวข้องเป็นจำนวนเต็มที่ไม่เป็นลบเรียกว่าพหุนาม

\(x^3+ x^2 + 2x + 1\) คือพหุนามในตัวแปร x หนึ่งตัว
\(6x - \frac{4x}{y} + 2y + 3 \) ไม่ใช่พหุนาม (สังเกตว่า y ในเทอมที่สองยกกำลัง -1)

การบวกและการลบเงื่อนไขการถูกใจ

หากต้องการรวมคำศัพท์ที่เหมือนกันด้วยการบวกหรือลบ เพียงเพิ่มหรือลบค่าสัมประสิทธิ์ตัวเลขของคำศัพท์ที่กำหนด
ตัวอย่าง:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

การบวกและการลบนิพจน์พีชคณิต

หากต้องการเพิ่มนิพจน์เกี่ยวกับพีชคณิต เพียงเพิ่มเงื่อนไขที่เหมือนกัน เพื่อความสะดวก ให้เขียนคำที่คล้ายกันไว้ใต้อีกคำในคอลัมน์เดียวกัน ตัวอย่าง:
เพิ่ม -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

สำหรับ การลบ ให้ พลิกเครื่องหมายของแต่ละเทอมของนิพจน์ที่กำลังลบออก แล้วบวกทั้งสองนิพจน์เข้าด้วยกัน ตัวอย่าง
ลบ \(3x^2 + 5x + 7y^2\) จาก \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

คุณยังสามารถเพิ่มหรือลบนิพจน์พีชคณิตโดยใช้ การจัดกลุ่ม ลองใช้ตัวอย่างข้างต้นแล้วลบโดยใช้การจัดกลุ่ม:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

การคูณนิพจน์พีชคณิต

การคูณนิพจน์พีชคณิตสามารถแบ่งออกเป็นสามกรณี เรามาคุยกันแยกกัน:

กรณี ฉัน (การคูณของ Monomials) : คูณค่าสัมประสิทธิ์ตัวเลขเข้าด้วยกันแล้วคูณกับตัวแปรโดยการเพิ่มเลขยกกำลังของตัวแปรทั่วไป ปล่อยให้ตัวแปรที่ไม่ธรรมดาไม่เปลี่ยนแปลง ตัวอย่าง: ค้นหาผลคูณของ 6bc และ 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

กรณี ครั้งที่สอง (การคูณพหุนามด้วยโมโนเมียล) : คูณแต่ละพจน์ของพหุนามด้วยโมโนเมียล ตัวอย่าง: ผลคูณของ 3xy และ x ² + 2xy + y ² คือ
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

กรณี สาม (การคูณพหุนามด้วยพหุนาม) : คูณแต่ละพจน์ของพหุนามหนึ่งด้วยทุก ๆ พจน์ของอีกพจน์หนึ่ง แล้วรวมพจน์ที่เหมือนกันเพื่อลดความซับซ้อนของผลคูณ ตัวอย่าง: ผลคูณของ (2x + 3y) และ ( x + y + 2) คือ
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

การแบ่งนิพจน์พีชคณิต

การแบ่งนิพจน์พีชคณิตสามารถอธิบายได้โดยใช้สามกรณีด้านล่าง

กรณี ฉัน (การหาร monomial โดย monomial) : ในการหาร monomial ด้วย monomial ให้หาผลหารของสัมประสิทธิ์ตัวเลขและผลหารของตัวแปรโดยการลบเลขชี้กำลังของตัวแปรทั่วไป ตัวอย่าง:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

กรณี ครั้งที่สอง (Division of Polynomial by Monomial) : นำพจน์ของพหุนามมาหารด้วย monomial แล้วหารตามตัวอย่างข้างต้น
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

กรณี สาม ( การหารพหุนามด้วยพหุนาม ): จะทำโดยวิธีหารยาว ให้เราพยายามทำความเข้าใจโดยใช้ตัวอย่าง
\(8x^2 + 9x - 8 \div 8x + 1\)

เริ่มต้นด้วยการหารพจน์แรกของเงินปันผล (8x ² ) ด้วยพจน์แรกของตัวหาร (8x) เพื่อหาพจน์แรกของผลหาร (x) จากนั้นคุณคูณพจน์ผลหารกับตัวหารและลบออก

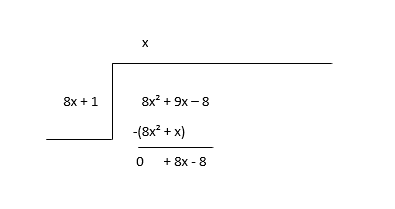
พิจารณาส่วนที่เหลือเป็นเงินปันผลใหม่และประมาณการระยะถัดไปของผลหาร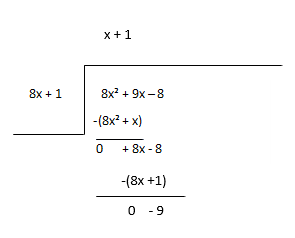

ผลหาร - x + 1 ส่วนที่เหลือ - -9

การลบวงเล็บเหลี่ยมและการใช้กฎลำดับการดำเนินการ

หากต้องการลดความซับซ้อนของนิพจน์พีชคณิตที่มีวงเล็บ ให้ถอดวงเล็บออกตามลำดับดังนี้

ตัวอย่าง:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)