Back to the topics list

algebraic expression

Nilalaman:

• Ano ang isang Variable?
• Mga Uri ng Algebraic Expression.
• Coefficient.
• Mga Tuntunin ng Like at Unlike.
• Polinomyal.
• Addition, Subtraction, Multiplication at Division of Algebraic expression.
• Application ng Order of Operations rule para gawing simple ang Algebraic expression.

Mga Literal na Numero

Sa Algebra ginagamit namin ang English o Greek Alphabets tulad ng a, b, x, y, β, Φ, ... upang kumatawan sa mga numero. Ang mga titik na ito ay ginagamit upang kumatawan sa hindi kilalang dami. Dahil ang mga titik ay kumakatawan sa mga numero kaya tinawag silang literal na mga numero. Ang isang literal na numero ay maaaring maglagay ng anumang halaga kaya tinatawag namin itong isang variable . Ang isang numero na may isang tiyak na halaga ay tinatawag na isang pare-pareho.

Algebraic expression

Ang kumbinasyon ng mga constant at literal(mga variable) na konektado ng isa o higit pang aritmetika na operasyon(pagdaragdag, pagpaparami, pagbabawas, paghahati) ay tinatawag na Algebraic expression. Ang isa o higit pang mga palatandaan (+, −) ay naghiwa-hiwalay ng algebraic expression sa ilang bahagi. Ang bawat bahagi na may sign nito ay tinatawag na termino ng algebraic expression. Ang isang termino ay maaaring maging isang pare-pareho tulad ng halimbawa 4, isang variable, halimbawa, x, isang produkto ng isang pare-pareho at variable, halimbawa, 4x o isang produkto ng dalawa o higit pang mga variable, halimbawa, xy, xy ² .

Monomial: Ang isang algebraic expression na may isang term lamang ay tinatawag na monomial. Halimbawa: 7x, ab ² , 8
Binomial: Ang isang algebraic expression na may dalawang termino ay tinatawag na binomial. Halimbawa: x ² + y ² , x + 2
Trinomial: Ang isang algebraic expression na may tatlong termino ay tinatawag na trinomial. Halimbawa: x ² + y ² + z ² , x +y +2

Coefficient

Ang bawat isa sa mga dami (constant o literal) na pinarami upang bumuo ng isang produkto, ay tinatawag na isang kadahilanan ng produkto at anumang kadahilanan sa isang produkto ay tinatawag na koepisyent ng produkto ng natitirang mga kadahilanan. Sa termino, -11p ² q ng expression na 5p ³ − 11p ² q + 7,

• Ang numerical coefficient ay -11.
• Ang literal na koepisyent ay p ² q.
• Ang koepisyent ng p ² ay -11q.
• Ang koepisyent ng -11p ² ay q.
  

Mga Tuntunin ng Like at Unlike

Ang mga termino ng algebraic expression na may parehong (mga) variable at parehong exponent(s) ng mga variable ay sinasabing katulad ng mga termino. Tulad ng termino ay maaaring mag-iba lamang sa mga coefficient.
2xy+ 3x + 4y + 5xy + 7y
Ang mga terminong 2xy at 5xy ay parang mga termino. Ang 4y at 7y ay parang mga termino.

Ang mga termino sa algebraic expression na 2x + 3xy + 5y ay lahat ay hindi katulad.

Polinomyal

Ang isang algebraic expression kung saan ang mga kapangyarihan ng mga variable na kasangkot ay hindi negatibong integer ay tinatawag na polynomial.

\(x^3+ x^2 + 2x + 1\) ay isang polynomial sa isang variable na x.
\(6x - \frac{4x}{y} + 2y + 3 \) ay hindi isang polynomial (pansinin na ang y sa pangalawang termino ay may kapangyarihan -1)

Pagdaragdag at Pagbabawas ng Mga Katulad na Tuntunin

Upang pagsamahin ang mga katulad na termino sa pamamagitan ng pagdaragdag o pagbabawas, idagdag o ibawas lamang ang mga numerical coefficient ng mga ibinigay na termino.
Halimbawa:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Pagdaragdag at Pagbabawas ng Algebraic Expressions

Upang magdagdag ng algebraic expression, idagdag lang ang mga katulad nilang termino. Para sa kaginhawaan, isulat ang katulad na termino sa ibaba ng isa sa parehong hanay. Halimbawa:
Magdagdag ng -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Para sa pagbabawas , i-flip ang sign ng bawat termino ng expression na ibinabawas at pagkatapos ay pagsamahin ang dalawang expression. Halimbawa
Ibawas ang \(3x^2 + 5x + 7y^2\) sa \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Maaari ka ring magdagdag o magbawas ng mga algebraic na expression gamit ang Pagpapangkat. Kunin natin ang halimbawa sa itaas at ibawas gamit ang Pagpapangkat:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Multiplikasyon ng Algebraic Expressions

Ang multiplikasyon ng algebraic expression ay maaaring nahahati sa tatlong kaso, pag-usapan natin ang mga ito nang hiwalay:

Kaso ako (Multiplication of Monomials) : I-multiply ang kanilang mga numerical coefficient nang magkasama at pagkatapos ay ang mga variable sa pamamagitan ng pagdaragdag ng mga exponents ng mga karaniwang variable, na iniiwan ang mga hindi karaniwang variable na hindi nagbabago. Halimbawa: Hanapin ang produkto ng 6bc at 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Kaso II (Multiplication Polynomial sa isang Monomial) : I-multiply ang bawat termino ng polynomial sa monomial. Halimbawa: Ang produkto ng 3xy at x ² + 2xy + y ² ay
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Kaso III (Multiplication of a Polynomial by Polynomial) : I-multiply ang bawat term ng isang polynomial sa bawat term ng isa at pagkatapos ay pagsamahin ang mga katulad na termino para gawing simple ang produkto. Halimbawa: Ang produkto ng (2x + 3y) at ( x + y + 2) ay
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Dibisyon ng Algebraic Expressions

Ang dibisyon ng algebraic expression ay maaaring ipaliwanag gamit ang ibaba ng tatlong kaso.

Kaso ako (Division of a Monomial by a Monomial) : Upang hatiin ang isang monomial sa isang monomial, hanapin ang mga quotient ng kanilang mga numerical coefficient at ang mga quotient ng mga variable sa pamamagitan ng pagbabawas sa mga exponent ng mga karaniwang variable. Halimbawa:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Kaso II (Dibisyon ng Polynomial sa Monomial) : Hatiin ang bawat termino ng polynomial sa monomial at pagkatapos ay hatiin tulad ng ibinigay sa kaso sa itaas. Halimbawa:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Kaso III ( Division of a Polynomial by a Polynomial ): Ito ay gagawin sa pamamagitan ng long division method. Subukan nating maunawaan ito gamit ang isang halimbawa.
\(8x^2 + 9x - 8 \div 8x + 1\)

Magsimula sa pamamagitan ng paghahati sa unang termino ng dibidendo(8x ² ) sa unang termino ng divisor(8x) upang mahanap ang unang termino ng quotient(x) at pagkatapos ay i-multiply mo ang quotient term sa divisor at ibawas.

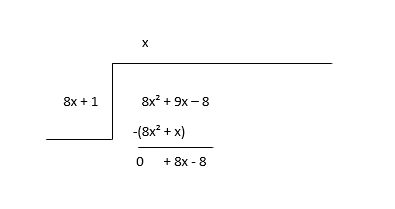
Isaalang-alang ang natitira bilang bagong dibidendo at tantyahin ang susunod na termino ng quotient.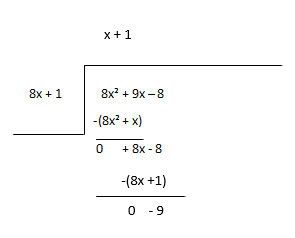

Quotient - x + 1, Natitira - -9

Pag-alis ng mga Bracket at paggamit ng Order of Operations Rule

Upang gawing simple ang isang algebraic expression na naglalaman ng mga bracket, alisin ang mga bracket sa pagkakasunud-sunod ng :

Halimbawa:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)