Back to the topics list

cebirsel ifade

içindekiler:

• Değişken nedir?
• Cebirsel İfade Türleri.
• katsayı.
• Beğenme ve Beğenmeme Terimleri.
• Polinom.
• Cebirsel ifadelerde Toplama, Çıkarma, Çarpma ve Bölme.
• Cebirsel ifadeyi basitleştirmek için İşlem Sırası kuralının uygulanması.

Değişmez Sayılar

Cebirde sayıları temsil etmek için a, b, x, y, β, Φ, ... gibi İngiliz veya Yunan Alfabelerini kullanırız. Bu harfler bilinmeyen miktarları temsil etmek için kullanılır. Harfler sayıları temsil ettiği için bunlara değişmez sayılar denir. Sabit bir sayı herhangi bir değeri alabilir, bu nedenle ona değişken diyoruz. Belirli bir değeri olan bir sayıya sabit denir.

Cebirsel ifade

Bir veya daha fazla aritmetik işlemle (toplama, çarpma, çıkarma, bölme) birbirine bağlanan sabitlerin ve değişmezlerin (değişkenlerin) birleşimine Cebirsel ifade denir. Bir veya daha fazla işaret (+, -) bir cebirsel ifadeyi birkaç parçaya böler. İşareti olan her parçaya cebirsel ifadenin bir terimi denir. Bir terim, örneğin 4 gibi bir sabit, bir değişken, örneğin x, bir sabit ve değişkenin çarpımı, örneğin 4x veya iki veya daha fazla değişkenin çarpımı, örneğin xy, ^xy2 olabilir.

Tek terimli: Yalnızca bir terimi olan bir cebirsel ifadeye tek terimli denir. Örnek: 7x, ab ² , 8
Binom: İki terimi olan bir cebirsel ifadeye binom denir. Örnek: x ² + y ² , x + 2
Üç terimli : Üç terimi olan bir cebirsel ifadeye üç terimli denir. Örnek: x ² + y ² + z ² , x +y +2

katsayı

Bir çarpımı oluşturmak için çarpılan niceliklerin (sabit veya değişmez değerlerin) her birine ürünün çarpanı denir ve bir çarpımdaki herhangi bir faktöre kalan faktörlerin çarpımının katsayısı denir. 5p ³ − 11p ² q + 7 ifadesinin -11p ² q teriminde,

• Sayısal katsayı -11'dir.
• Değişmez katsayı p ² q'dur.
• p ^2'nin katsayısı -11q'dir.
• -11p ^2'nin katsayısı q'dur.
  

Beğenme ve Beğenmeme Terimleri

Aynı değişken(ler)e ve değişkenlerin aynı üs(ler)ine sahip cebirsel ifadenin terimlerine benzer terimler denir. Benzer terim sadece katsayılarda farklılık gösterebilir.
2xy+ 3x + 4y + 5xy + 7y
2xy ve 5xy terimleri benzer terimlerdir. 4y ve 7y benzer terimlerdir.

2x + 3xy + 5y cebirsel ifadesindeki terimlerin tümü birbirine benzemez.

Polinom

İlgili değişkenlerin kuvvetlerinin negatif olmayan tamsayılar olduğu bir cebirsel ifadeye polinom denir.

\(x^3+ x^2 + 2x + 1\) , x değişkenli bir polinomdur.
\(6x - \frac{4x}{y} + 2y + 3 \) bir polinom değildir (ikinci terimdeki y'nin -1 gücüne sahip olduğuna dikkat edin)

Benzer Terimlerin Toplama ve Çıkarma

Benzer terimleri toplama veya çıkarma yoluyla birleştirmek için verilen terimlerin sayısal katsayılarını toplayın veya çıkarın.
Örnek:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Cebirsel İfadelerde Toplama ve Çıkarma

Cebirsel ifade eklemek için, onlarınkine benzer terimleri eklemeniz yeterlidir. Kolaylık sağlamak için, benzer terimleri aynı sütunda alt alta yazın. Örnek:
Ekle -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Çıkarma için, çıkarılan ifadenin her bir teriminin işaretini çevirin ve ardından iki ifadeyi birlikte toplayın. Örnek
\(9x^2 + 7x + 5y + 10y^2\) \(3x^2 + 5x + 7y^2\) 'yi çıkarın

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Gruplamayı kullanarak cebirsel ifadeler de ekleyebilir veya çıkarabilirsiniz. Yukarıdaki örneği ele alalım ve Gruplamayı kullanarak çıkaralım:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Cebirsel İfadelerin Çarpımı

Cebirsel ifadenin çarpımı üç duruma ayrılabilir, bunları ayrı ayrı tartışalım:

Dava ben (Tek terimlilerin Çarpımı) : Sayısal katsayılarını birlikte ve ardından yaygın olmayan değişkenleri değiştirmeden bırakarak ortak değişkenlerin üslerini toplayarak değişkenleri çarpın. Örnek: 6bc ile 5b'nin çarpımını bulun = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Dava III (Bir Monom ile Çarpma Polinomu) : Polinomun her bir terimini tek terimli ile çarpın. Örnek: 3xy ve x ² + 2xy + y ^2'nin çarpımı
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Dava III (Bir Polinomun Polinomla Çarpılması) : Bir polinomun her terimini diğerinin her terimiyle çarpın ve ardından benzer terimleri birleştirerek çarpımı sadeleştirin. Örnek: (2x + 3y) ve ( x + y + 2)'nin çarpımı
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Cebirsel İfadelerin Bölünmesi

Cebirsel ifadenin bölünmesi aşağıdaki üç durum kullanılarak açıklanabilir.

Dava ben (Tek terimlinin bir Tek terimliye bölünmesi) : Bir tek terimliyi bir tek terimliye bölmek için, ortak değişkenlerin üslerini çıkararak sayısal katsayılarının bölümlerini ve değişkenlerin bölümlerini bulun.Örnek:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Dava III (Polinomun Monomiyele Bölünmesi) : Polinomun her bir terimini bir tek terime bölün ve ardından yukarıdaki durumda verildiği gibi bölün.Örnek:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Dava III ( Polinomun Polinomla Bölünmesi ): Bu, uzun bölme yöntemiyle yapılacaktır. Bunu bir örnek üzerinden anlamaya çalışalım.
\(8x^2 + 9x - 8 \div 8x + 1\)

Bölümün (x) ilk terimini bulmak için bölenin (8x ² ) ilk terimini bölenin (8x) ilk terimine bölerek başlayın ve ardından bölüm terimini bölenle çarpıp çıkarın.

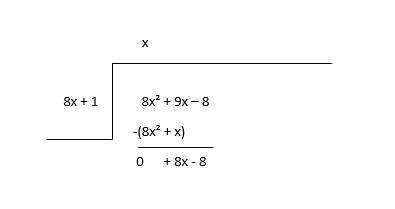
Kalanı yeni temettü olarak kabul edin ve bölümün bir sonraki terimini tahmin edin.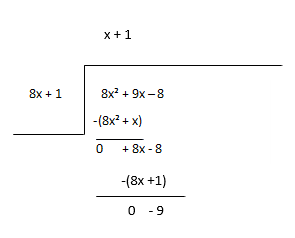

Bölüm - x + 1, Kalan - -9

Parantezlerin Kaldırılması ve İşlem Sırası Kuralının Kullanılması

Köşeli parantez içeren bir cebirsel ifadeyi basitleştirmek için köşeli parantezleri şu sırayla kaldırın:

Örnek:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)