Back to the topics list

алгебраїчний вираз

Зміст:

• Що таке змінна?
• Типи алгебраїчного виразу.
• Коефіцієнт.
• Умови «подобається» та «не подобається».
• Поліном.
• Додавання, віднімання, множення та ділення алгебраїчного виразу.
• Застосування правила порядку операцій для спрощення алгебраїчного виразу.

Літеральні числа

В алгебрі ми використовуємо англійські або грецькі алфавіти, такі як a, b, x, y, β, Φ, ... для представлення чисел. Ці літери використовуються для позначення невідомих величин. Оскільки літери представляють числа, їх називають літеральними числами. Літеральне число може приймати будь-яке значення, тому ми називаємо його змінною . Число з певним значенням називається константою.

Алгебраїчний вираз

Комбінація констант і літералів (змінних), з’єднаних однією або кількома арифметичними операціями (додавання, множення, віднімання, ділення), називається алгебраїчним виразом. Один або кілька знаків (+, −) розбивають алгебраїчний вираз на кілька частин. Кожна частина зі своїм знаком називається членом алгебраїчного виразу. Терм може бути константою, наприклад 4, змінною, наприклад, x, добутком константи та змінної, наприклад, 4x, або добутком двох чи більше змінних, наприклад, xy, xy ² .

Одночлен: алгебраїчний вираз, який має лише один член, називається мономом. Приклад: 7x, ab ² , 8
Біноміал: алгебраїчний вираз, який складається з двох членів, називається біноміалом. Приклад: x ² + y ² , x + 2
Тричлен: алгебраїчний вираз, який складається з трьох членів, називається тричленом. Приклад: x ² + y ² + z ² , x + y +2

Коефіцієнт

Кожна величина (константа або літерали), помножена на добуток, називається множником добутку, а будь-який множник у добутку називається коефіцієнтом добутку решти множників. У члені -11p ² q виразу 5p ³ − 11p ² q + 7,

• Числовий коефіцієнт -11.
• Літеральний коефіцієнт p ² q.
• Коефіцієнт p ² становить -11q.
• Коефіцієнт -11p ² дорівнює q.
  

Умови «подобається» та «не подобається».

Члени алгебраїчного виразу, що мають ту саму змінну(и) і той самий показник(и) змінних, називаються подібними термами. Подібний термін може відрізнятися лише коефіцієнтами.
2xy+ 3x + 4y + 5xy + 7y
Терми 2xy і 5xy схожі на терми. 4y і 7y подібні терміни.

Усі члени в алгебраїчному виразі 2x + 3xy + 5y є різними.

Поліном

Алгебраїчний вираз, у якому степені змінних є цілими невід’ємними числами, називається поліномом.

\(x^3+ x^2 + 2x + 1\) — поліном від однієї змінної x.
\(6x - \frac{4x}{y} + 2y + 3 \) не є поліномом (зверніть увагу, що y у другому члені має ступінь -1)

Додавання та віднімання подібних членів

Щоб поєднати однакові доданки шляхом додавання чи віднімання, просто додайте чи відніміть числові коефіцієнти даних доданків.
приклад:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Додавання і віднімання алгебраїчних виразів

Щоб додати алгебраїчний вираз, просто додайте їхні схожі терміни. Для зручності запишіть схожі терміни один під одним в одному стовпчику. приклад:
Додати -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Для віднімання переверніть знак кожного члена виразу, який віднімається, а потім додайте два вирази разом. приклад
Відніміть \(3x^2 + 5x + 7y^2\) із \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Ви також можете додавати або віднімати алгебраїчні вирази за допомогою групування. Давайте візьмемо наведений вище приклад і віднімемо за допомогою групування:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Множення алгебраїчних виразів

Множення алгебраїчного виразу можна розділити на три випадки, обговоримо їх окремо:

Справа я (Множення одночленів) : помножте їхні числові коефіцієнти, а потім змінні, додавши показники степенів загальних змінних, залишивши незвичайні змінні без змін. Приклад: Знайдіть добуток 6bc і 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Справа II (Множення многочлена на одночлен) : помножте кожен член многочлена на одночлен. Приклад: добуток 3xy і x ² + 2xy + y ² є
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Справа III (Множення многочлена на многочлен) : помножте кожен член одного многочлена на кожен член іншого, а потім об’єднайте подібні члени, щоб спростити добуток. Приклад: добуток (2x + 3y) і ( x + y + 2) є
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Поділ алгебраїчних виразів

Поділ алгебраїчного виразу можна пояснити за допомогою трьох наведених нижче випадків.

Справа я (Ділення одночлена на одночлен) : Щоб поділити одночлен на одночлен, знайдіть частки їхніх числових коефіцієнтів і частки змінних шляхом віднімання показників загальних змінних. Приклад:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Справа II (Ділення многочлена на одночлен) : розділіть кожен член многочлена на одночлен, а потім поділіть, як описано вище. Приклад:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Справа III ( Ділення многочлена на многочлен ): Це буде зроблено методом довгого ділення. Спробуємо розібратися в цьому на прикладі.
\(8x^2 + 9x - 8 \div 8x + 1\)

Почніть з ділення першого члена діленого (8x ² ) на перший член дільника (8x), щоб знайти перший член частки (x), а потім помножте частку на дільник і відніміть.

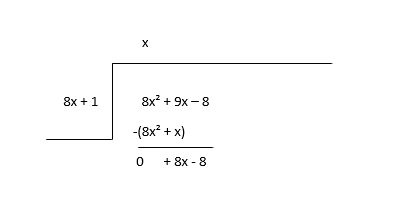
Вважайте залишок новим дивідендом і оцініть наступний термін частки.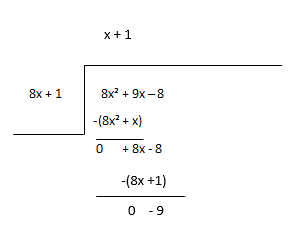

Частка - х + 1, остача - -9

Зняття дужок і використання правила порядку операцій

Щоб спростити алгебраїчний вираз, що містить дужки, видаліть дужки в такому порядку:

приклад:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)