Back to the topics list

الجبری اظہار

مشمولات:

• متغیر کیا ہے؟
• الجبری اظہار کی اقسام۔
• عددی سر.
• پسند اور ناپسند کی شرائط۔
• کثیر الثانی۔
• الجبری اظہار کا اضافہ، گھٹاؤ، ضرب اور تقسیم۔
• الجبری اظہار کو آسان بنانے کے لیے آرڈر آف آپریشنز کے اصول کا اطلاق۔

لغوی نمبر

الجبرا میں ہم اعداد کی نمائندگی کے لیے انگریزی یا یونانی حروف تہجی جیسے a, b, x, y, β, Φ, ... استعمال کرتے ہیں۔ یہ حروف نامعلوم مقداروں کی نمائندگی کے لیے استعمال ہوتے ہیں۔ چونکہ حروف اعداد کی نمائندگی کرتے ہیں اس لیے انہیں لغوی نمبر کہا جاتا ہے۔ ایک لغوی نمبر کسی بھی قدر کو فرض کر سکتا ہے اس لیے ہم اسے متغیر کہتے ہیں۔ ایک مقررہ قدر کے ساتھ عدد کو مستقل کہا جاتا ہے۔

الجبری اظہار

ایک یا زیادہ ریاضی کی کارروائیوں (اضافہ، ضرب، گھٹاؤ، تقسیم) کے ذریعہ متغیرات اور لٹریلز (متغیرات) کا مجموعہ الجبری اظہار کہلاتا ہے۔ ایک یا زیادہ علامات (+, −) ایک الجبری اظہار کو کئی حصوں میں توڑ دیتے ہیں۔ ہر حصے کو اس کے نشان کے ساتھ الجبری اظہار کی اصطلاح کہا جاتا ہے۔ ایک اصطلاح ایک مستقل ہو سکتی ہے جیسے مثال کے طور پر 4، ایک متغیر، مثال کے طور پر، x، ایک مستقل اور متغیر کی پیداوار، مثال کے طور پر، 4x یا دو یا دو سے زیادہ متغیرات کی پیداوار، مثال کے طور پر، xy، xy ² ۔

Monomial: ایک الجبری اظہار جس میں صرف ایک اصطلاح ہو اسے monomial کہتے ہیں۔ مثال: 7x، ab ² ، 8
بائنومیئل: ایک الجبری اظہار جس میں دو اصطلاحات ہوں اسے binomial کہتے ہیں۔ مثال: x ² + y ² ، x + 2
تثلیث: ایک الجبری اظہار جس میں تین اصطلاحات ہوں اسے تثلیث کہا جاتا ہے۔ مثال: x ² + y ² + z ² , x +y +2

عددی سر

مقدار (مستقل یا لغوی) میں سے ہر ایک کو ایک مصنوعہ بنانے کے لیے ضرب کیا جاتا ہے، اسے مصنوع کا عنصر کہا جاتا ہے اور کسی مصنوع میں کسی بھی عنصر کو باقی عوامل کی پیداوار کا عدد کہا جاتا ہے۔ اصطلاح میں، -11p ² q اظہار 5p ³ − 11p ² q + 7،

• عددی گتانک -11 ہے۔
• لفظی گتانک p ² q ہے۔
• p ² کا عدد -11q ہے۔
• -11p ² کا عدد q ہے۔
  

پسند اور ناپسند کی شرائط

الجبری ایکسپریشن کی اصطلاحات جن میں متغیرات کے ایک ہی متغیر اور ایک ہی ایکسپونٹ (s) ہوتے ہیں ان کو اصطلاحات کی طرح کہا جاتا ہے۔ جیسے اصطلاح صرف گتانک میں مختلف ہو سکتی ہے۔
2xy + 3x + 4y + 5xy + 7y
اصطلاحات 2xy اور 5xy اصطلاحات کی طرح ہیں۔ 4y اور 7y اصطلاحات کی طرح ہیں۔

الجبری ایکسپریشن 2x + 3xy + 5y کی اصطلاحات سب کے برعکس ہیں۔

کثیر الثانی

ایک الجبری اظہار جس میں متغیرات کی طاقتیں شامل ہیں غیر منفی عدد کو کثیر الثانی کہا جاتا ہے۔

\(x^3+ x^2 + 2x + 1\) ایک متغیر x میں کثیر الجہتی ہے۔
\(6x - \frac{4x}{y} + 2y + 3 \) ایک کثیر نام نہیں ہے (دیکھیں کہ دوسری اصطلاح میں y کی طاقت -1 ہے)

پسند کی شرائط کا اضافہ اور گھٹاؤ

جمع یا گھٹا کر جیسی اصطلاحات کو یکجا کرنے کے لیے، صرف دی گئی اصطلاحات کے عددی گتانک کو جوڑیں یا گھٹائیں۔
مثال:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

الجبری تاثرات کا اضافہ اور گھٹاؤ

الجبری اظہار کو شامل کرنے کے لیے، صرف ان کی اصطلاحات کی طرح شامل کریں۔ سہولت کے لیے اسی کالم میں اسی طرح کی اصطلاح ایک دوسرے کے نیچے لکھیں۔ مثال:
شامل کریں -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) \(2x + 4xy + y\) \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

گھٹانے کے لیے، اظہار کی ہر اصطلاح کے نشان کو پلٹائیں جو منہا کیا جا رہا ہے اور پھر دونوں اظہار کو ایک ساتھ جوڑ دیں۔ مثال
گھٹائیں \(3x^2 + 5x + 7y^2\) سے \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

آپ گروپنگ کا استعمال کرتے ہوئے الجبری اظہار کو شامل یا گھٹا بھی سکتے ہیں۔ آئیے اوپر کی مثال لیں اور گروپنگ کا استعمال کرتے ہوئے منہا کریں:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

الجبری تاثرات کی ضرب

الجبری اظہار کی ضرب کو تین صورتوں میں تقسیم کیا جا سکتا ہے، آئیے ان پر الگ الگ بات کرتے ہیں:

معاملہ میں (Multiplication of Monomials) : ان کے عددی گتانکوں کو ایک ساتھ ضرب دیں اور پھر عام متغیرات کے ایکسپوننٹ کو شامل کر کے، غیر معمولی متغیرات کو بغیر کسی تبدیلی کے چھوڑ دیں۔ مثال: 6bc اور 5b = کی پیداوار تلاش کریں۔ \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

معاملہ II (اضافہ کثیر الجہتی بذریعہ یک واحد) : کثیر الاضلاع کی ہر اصطلاح کو یکجہتی سے ضرب دیں۔ مثال: 3xy اور x ² + 2xy + y ² کی پیداوار ہے۔
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

معاملہ III (کثیریت کی ضرب از کثیر) : ایک کثیر الاضلاع کی ہر اصطلاح کو دوسرے کی ہر اصطلاح سے ضرب دیں اور پھر مصنوعات کو آسان بنانے کے لیے ان جیسی اصطلاحات کو ملا دیں۔ مثال: (2x + 3y) اور (x + y + 2) کی پیداوار ہے۔
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

الجبری اظہار کی تقسیم

ذیل میں تین صورتوں کا استعمال کرتے ہوئے الجبری اظہار کی تقسیم کی وضاحت کی جا سکتی ہے۔

معاملہ میں (ایک یکی کی تقسیم بذریعہ یک واحد) : یک نامی کو یکی سے تقسیم کرنے کے لیے، ان کے عددی گتانک اور متغیرات کے اقتباسات کو مشترک متغیرات کے اخراج کو گھٹا کر تلاش کریں۔ مثال:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

معاملہ II (کثیریت کی تقسیم بذریعہ یکی) : کثیر الاضلاع کی ہر اصطلاح کو یک نامی سے تقسیم کریں اور پھر تقسیم کریں جیسا کہ اوپر دی گئی صورت میں دی گئی ہے۔ مثال:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

معاملہ III ( ایک کثیر نام کی طرف سے ایک کثیر نام کی تقسیم ): یہ طویل تقسیم کے طریقہ کار سے کیا جائے گا۔ آئیے ایک مثال کے ذریعے اسے سمجھنے کی کوشش کرتے ہیں۔
\(8x^2 + 9x - 8 \div 8x + 1\)

ڈیویڈنڈ کی پہلی اصطلاح (8x ² ) کو تقسیم کرنے والے کی پہلی اصطلاح (8x) کے ساتھ تقسیم کرکے حصہ (x) کی پہلی اصطلاح معلوم کرنے کے لیے شروع کریں اور پھر آپ اقتباس کی اصطلاح کو تقسیم کرنے والے کے ساتھ ضرب کریں اور گھٹائیں۔

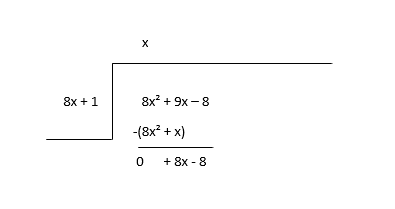
بقیہ کو نئے ڈیویڈنڈ کے طور پر سمجھیں اور حصص کی اگلی مدت کا اندازہ لگائیں۔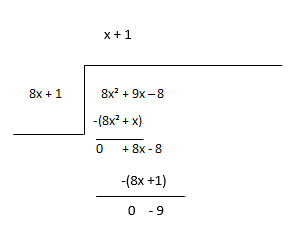

مقدار - x + 1، باقی - -9

بریکٹ کو ہٹانا اور آرڈر آف آپریشنز رول کا استعمال

بریکٹ پر مشتمل الجبری اظہار کو آسان بنانے کے لیے، بریکٹ کو اس ترتیب سے ہٹا دیں:

مثال:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)