Back to the topics list

algebraik ifoda

Tarkib:

• O'zgaruvchi nima?
• Algebraik ifoda turlari.
• Koeffitsient.
• Yoqtirish va yoqtirmaslik shartlari.
• Polinom.
• Algebraik ifodani qo‘shish, ayirish, ko‘paytirish va bo‘lish.
• Algebraik ifodani soddalashtirish uchun amallar tartibi qoidasini qo'llash.

Literal raqamlar

Algebrada raqamlarni ifodalash uchun a, b, x, y, b, p, ... kabi ingliz yoki yunon alifbolaridan foydalanamiz. Bu harflar noma'lum miqdorlarni ifodalash uchun ishlatiladi. Harflar raqamlarni ifodalaganligi sababli ular harflar deb ataladi. Literal raqam har qanday qiymatni qabul qilishi mumkin, shuning uchun biz uni o'zgaruvchi deb ataymiz. Aniq qiymatga ega bo'lgan son doimiy deb ataladi.

Algebraik ifoda

Bir yoki bir nechta arifmetik amallar (qo‘shish, ko‘paytirish, ayirish, bo‘lish) orqali bog‘langan doimiy va literallar (o‘zgaruvchilar) birikmasi algebraik ifoda deyiladi. Bir yoki bir nechta belgilar (+, -) algebraik ifodani bir necha qismlarga ajratadi. Har bir qism o'z belgisi bilan algebraik ifodaning hadi deb ataladi. Termin, masalan, 4, o'zgaruvchi, masalan, x, doimiy va o'zgaruvchining mahsuloti, masalan, 4x yoki ikki yoki undan ortiq o'zgaruvchilarning ko'paytmasi, masalan, xy, xy ² kabi doimiy bo'lishi mumkin.

Monomial: Faqat bitta atamasi bo'lgan algebraik ifoda monomial deyiladi. Misol: 7x, ab ² , 8
Binom: Ikki haddan iborat algebraik ifoda binomial deyiladi. Misol: x ² + y ² , x + 2
Trinomial: Uch a'zodan iborat algebraik ifoda trinomiyali deyiladi. Misol: x ² + y ² + z ² , x +y +2

Koeffitsient

Mahsulot hosil qilish uchun ko'paytiriladigan miqdorlarning har biri (doimiy yoki literal) mahsulot omili deb ataladi va mahsulotdagi har qanday omil qolgan omillar mahsulotining koeffitsienti deb ataladi. Termada 5p ³ − 11p ² q + 7 ifodaning -11p ² q,

• Raqamli koeffitsient -11.
• Literal koeffitsient p ² q.
• p ² koeffitsienti -11q.
• -11p ² koeffitsienti q.
  

Yoqtirish va yoqtirmaslik shartlari

O'zgaruvchilarning bir xil o'zgaruvchi(lari) va ko'rsatkich(lari)ga ega bo'lgan algebraik ifodaning hadlari atamalar deyiladi. Xuddi shunday atama faqat koeffitsientlarda farq qilishi mumkin.
2xy+ 3x + 4y + 5xy + 7y
2xy va 5xy atamalar atamalarga o'xshaydi. 4y va 7y atamalarga o'xshaydi.

2x + 3xy + 5y algebraik ifodadagi atamalarning barchasi bir-biriga o'xshamaydi.

Polinom

Ishtirok etgan o'zgaruvchilarning darajalari manfiy bo'lmagan butun sonlar bo'lgan algebraik ifoda ko'phad deyiladi.

\(x^3+ x^2 + 2x + 1\) bir x oʻzgaruvchidagi koʻphaddir.
\(6x - \frac{4x}{y} + 2y + 3 \) polinom emas (ikkinchi haddagi y ning -1 darajasiga ega ekanligiga e'tibor bering)

O'xshash atamalarni qo'shish va ayirish

O'xshash atamalarni qo'shish yoki ayirish yo'li bilan birlashtirish uchun berilgan atamalarning sonli koeffitsientlarini qo'shish yoki ayirish kifoya.
Misol:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Algebraik ifodalarni qo‘shish va ayirish

Algebraik ifodani qo'shish uchun ularga o'xshash atamalarni qo'shing. Qulaylik uchun xuddi shu ustunga o'xshash atamalarni bir-birining ostiga yozing. Misol:
Qo'shish -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Ayirish uchun ayirilayotgan ifodaning har bir aʼzosining belgisini aylantiring va keyin ikkita ifodani qoʻshing. Misol
\(3x^2 + 5x + 7y^2\) dan \(9x^2 + 7x + 5y + 10y^2\) ayiring.

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Guruhlash yordamida algebraik ifodalarni qo‘shish yoki ayirish ham mumkin. Yuqoridagi misolni olaylik va Guruhlash yordamida ayiramiz:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Algebraik ifodalarni ko‘paytirish

Algebraik ifodani ko'paytirishni uchta holatga bo'lish mumkin, keling, ularni alohida ko'rib chiqamiz:

Case I (Monomiylarni ko'paytirish) : Ularning sonli koeffitsientlarini, so'ngra umumiy o'zgaruvchilarning ko'rsatkichlarini qo'shish orqali o'zgaruvchilarni ko'paytiring, kam uchraydigan o'zgaruvchilarni o'zgarishsiz qoldiring. Misol: 6bc va 5b = ko'paytmasini toping \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Case II (Ko‘pnomni monomga ko‘paytirish) : Ko‘phadning har bir hadini monomga ko‘paytiring. Misol: 3xy va x ² + 2xy + y ² ko'paytmasi
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Case III (Ko‘pnomni ko‘pnomga ko‘paytirish) : Bir ko‘phadning har bir hadini ikkinchisining har bir hadiga ko‘paytiring va keyin hosilni soddalashtirish uchun shunga o‘xshash shartlarni birlashtiring. Misol: (2x + 3y) va (x + y + 2) ko'paytmasi
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Algebraik ifodalar bo'limi

Algebraik ifodaning bo'linishini quyidagi uchta holatdan foydalanib tushuntirish mumkin.

Case I (Monomialni monomga bo'lish) : Monomialni monomga bo'lish uchun umumiy o'zgaruvchilarning darajalarini ayirish yo'li bilan ularning son koeffitsientlari va o'zgaruvchilarning koeffitsientlarini toping.Misol:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Case II (Koʻp aʼzoni bir nomga boʻlish) : Koʻphadning har bir aʼzosini monomga boʻling va keyin yuqoridagi holatda berilganidek boʻling. Misol:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Case III ( Ko'pnomni ko'p nomga bo'lish ): Bu uzoq bo'linish usuli bilan amalga oshiriladi. Keling, buni misol yordamida tushunishga harakat qilaylik.
\(8x^2 + 9x - 8 \div 8x + 1\)

Dividendning birinchi a'zosini (8x ² ) bo'linuvchining birinchi a'zosiga (8x) bo'lishdan boshlang, bo'linuvchining (x) birinchi hadini toping, so'ngra bo'linuvchini bo'luvchiga ko'paytiring va ayiring.

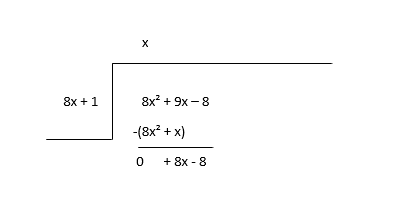
Qolgan qismini yangi dividend sifatida ko'rib chiqing va ko'rsatkichning keyingi muddatini taxmin qiling.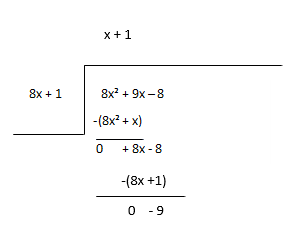

Quotient - x + 1, qoldiq - -9

Qavslarni olib tashlash va Operatsion tartib qoidalaridan foydalanish

Qavslarni o'z ichiga olgan algebraik ifodani soddalashtirish uchun qavslarni quyidagi tartibda olib tashlang:

Misol:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)