Back to the topics list

biểu thức đại số

nội dung:

• Biến là gì?
• Các loại biểu thức đại số.
• hệ số.
• Điều khoản thích và không thích.
• đa thức.
• Phép cộng, phép trừ, phép nhân và phép chia biểu thức đại số.
• Ứng dụng quy tắc thứ tự các phép toán để rút gọn biểu thức đại số.

số chữ

Trong Đại số, chúng ta sử dụng Bảng chữ cái tiếng Anh hoặc tiếng Hy Lạp như a, b, x, y, β, Φ, ... để biểu diễn các số. Những chữ cái này được sử dụng để đại diện cho số lượng chưa biết. Vì các chữ cái đại diện cho số nên chúng được gọi là số tự nhiên. Một số bằng chữ có thể nhận bất kỳ giá trị nào do đó chúng tôi gọi nó là một biến . Một số có giá trị xác định được gọi là một hằng số.

Biểu thức đại số

Một tổ hợp các hằng và hằng (biến) được kết nối bởi một hoặc nhiều phép toán số học (cộng, nhân, trừ, chia) được gọi là một biểu thức Đại số. Một hoặc nhiều dấu (+, -) chia một biểu thức đại số thành nhiều phần. Mỗi phần với dấu của nó được gọi là một số hạng của biểu thức đại số. Một số hạng có thể là một hằng số như ví dụ 4, một biến, chẳng hạn như x, tích của một hằng và biến, chẳng hạn như 4x hoặc tích của hai hay nhiều biến, chẳng hạn như xy, xy ² .

Đơn thức: Một biểu thức đại số chỉ có một hạng tử được gọi là đơn thức. Ví dụ: 7x, ab ² , 8
Nhị thức: Một biểu thức đại số có hai số hạng được gọi là nhị thức. Ví dụ: x ² + y ² , x + 2
Tam thức: Một biểu thức đại số có ba hạng tử được gọi là một tam thức. Ví dụ: x ² + y ² + z ² , x +y +2

hệ số

Mỗi đại lượng (hằng số hoặc hằng số) nhân với nhau để tạo thành một tích được gọi là một thừa số của tích và một thừa số bất kỳ trong một tích được gọi là hệ số của tích các thừa số còn lại. Trong số hạng -11p ² q của biểu thức 5p ³ − 11p ² q + 7,

• Hệ số là -11.
• Hệ số chữ là p ² q.
• Hệ số của p ² là -11q.
• Hệ số của -11p ² là q.
  

Điều khoản thích và không thích

Các số hạng của biểu thức đại số có cùng (các) biến và cùng (các) số mũ của các biến được gọi là các số hạng giống nhau. Thuật ngữ giống như chỉ có thể khác nhau về hệ số.
2xy+ 3x + 4y + 5xy + 7y
Các số hạng 2xy và 5xy giống các số hạng. 4y và 7y giống như các thuật ngữ.

Các số hạng trong biểu thức đại số 2x + 3xy + 5y đều không giống nhau.

đa thức

Một biểu thức đại số trong đó lũy thừa của các biến liên quan là các số nguyên không âm được gọi là đa thức.

\(x^3+ x^2 + 2x + 1\) là đa thức một biến x.
\(6x - \frac{4x}{y} + 2y + 3 \) không phải là đa thức (chú ý rằng y ở số hạng thứ hai có lũy thừa -1)

Cộng và trừ các điều khoản thích

Để kết hợp các số hạng giống nhau bằng cách cộng hoặc trừ, chỉ cần cộng hoặc trừ các hệ số bằng số của các số hạng đã cho.
Thí dụ:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Cộng và trừ các biểu thức đại số

Để thêm biểu thức đại số, chỉ cần thêm biểu thức tương tự của chúng. Để thuận tiện, hãy viết thuật ngữ tương tự bên dưới thuật ngữ kia trong cùng một cột. Thí dụ:
Thêm vào -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Đối với phép trừ , lật dấu của từng số hạng của biểu thức đang bị trừ và sau đó cộng hai biểu thức lại với nhau. Thí dụ
Trừ \(3x^2 + 5x + 7y^2\) khỏi \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Bạn cũng có thể cộng hoặc trừ các biểu thức đại số bằng cách sử dụng Nhóm. Hãy lấy ví dụ trên và trừ bằng cách sử dụng Nhóm:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Nhân các biểu thức đại số

Phép nhân biểu thức đại số có thể được chia thành ba trường hợp, hãy thảo luận riêng về chúng:

Trường hợp Tôi (Phép nhân các đơn thức) : Nhân các hệ số số của chúng với nhau và sau đó nhân các biến bằng cách cộng các số mũ của các biến thông thường, giữ nguyên các biến không phổ biến. Ví dụ: Tìm tích của 6bc và 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Trường hợp II (Nhân đa thức với một đơn thức) : Nhân mỗi hạng tử của đa thức với một đơn thức. Ví dụ: Tích của 3xy và x ² + 2xy + y ² là
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Trường hợp III (Phép nhân đa thức với đa thức) : Nhân mỗi hạng tử của đa thức này với mỗi hạng tử của đa thức kia rồi kết hợp các hạng tử giống nhau để rút gọn tích. Ví dụ: Tích của (2x + 3y) và ( x + y + 2) là
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Phép chia biểu thức đại số

Phép chia biểu thức đại số có thể được giải thích bằng ba trường hợp dưới đây.

Trường hợp Tôi (Chia một đơn thức cho một đơn thức) : Để chia một đơn thức cho một đơn thức, hãy tìm thương của các hệ số số của chúng và thương của các biến bằng cách trừ đi số mũ của các biến chung. Ví dụ:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Trường hợp II (Chia đa thức cho đơn thức) : Chia mỗi hạng tử của đa thức cho một đơn thức rồi chia như đã cho trong trường hợp trên. Ví dụ:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Trường hợp III ( Chia một đa thức cho một đa thức ): Điều này sẽ được thực hiện bằng phương pháp chia dài. Hãy để chúng tôi cố gắng hiểu điều này bằng cách sử dụng một ví dụ.
\(8x^2 + 9x - 8 \div 8x + 1\)

Bắt đầu bằng cách chia số hạng đầu tiên của số bị chia (8x ² ) với số hạng đầu tiên của số chia (8x) để tìm số hạng đầu tiên của thương (x) và sau đó bạn nhân số hạng thương với số chia và trừ.

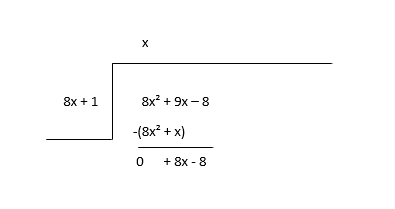
Coi phần còn lại là số bị chia mới và ước lượng số hạng tiếp theo của thương.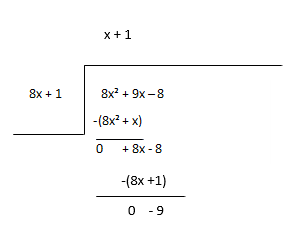

Thương - x + 1, Số dư - -9

Loại bỏ dấu ngoặc và sử dụng Quy tắc thứ tự hoạt động

Để đơn giản hóa biểu thức đại số có chứa dấu ngoặc, hãy loại bỏ dấu ngoặc theo thứ tự:

Thí dụ:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)