Er zijn drie fundamentele gaswetten (de wet van Boyle, de wet van Charles en de wet van Avogadro) die de relatie tussen druk, temperatuur, volume en hoeveelheid gas beschrijft. In deze les bespreken we het volgende:
Het is vernoemd naar Robert Boyle.
Dit stelt dat het volume omgekeerd evenredig is met de druk wanneer de temperatuur en het aantal moleculen constant zijn.
\(P ∝ 1/V\)
\(P = k_1V\)
waar,
P is de druk
V is het volume
en, k 1 is de evenredigheidsconstante
Als nu een vaste gasmassa een expansie ondergaat bij constante temperatuur, dan zullen het uiteindelijke volume en de uiteindelijke druk P 2 en V 2 zijn.
Het beginvolume en de begindruk zijn hier P 1 en V 1 , dan volgens de wet van Boyle:
\(P_1 \times V_1 = P_2 \times V_2 =constant (k_1) \)
\(or,\frac{P_1}{P_2} = \frac{V_2}{V_1} \)
Dus bij een constante temperatuur, als de druk wordt verdubbeld, wordt het volume van dat gas tot de helft verminderd. In vrije toestand neemt een gasvormige stof een groter volume van de container in vanwege de verstrooide moleculen. Wanneer er druk wordt uitgeoefend op de gasvormige stof, komen deze moleculen dichterbij en nemen ze een kleiner volume in. Met andere woorden, de toegepaste druk is recht evenredig met de dichtheid van het gas.
Hier is de grafische weergave van de wet van Boyle:
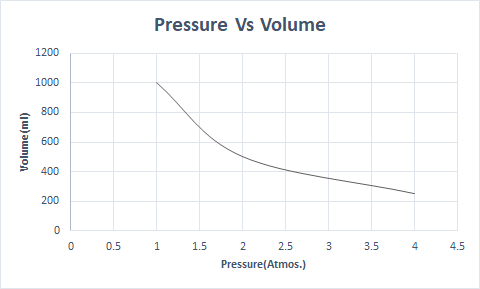
Op grotere hoogte is de atmosferische druk laag, dus de lucht is minder dicht. Als gevolg hiervan is er minder zuurstof beschikbaar om te ademen. Dit is de reden waarom bergbeklimmers zuurstofflessen dragen.
In 1787 bestudeerde Jacques Charles het effect van temperatuur op het volume van een gasvormige stof bij constante druk. De wet van Charles stelt dat bij constante druk en constante massa het volume van een gas recht evenredig is met de temperatuur.
\(V ∝ T\)
\(V = yT\)
Waarbij y een constante is, afhankelijk van de hoeveelheid gas en druk.
De wet van Charles wordt uitgedrukt als:
\(\frac{V_1}{T_1} = \frac{V_2}{T_2}\)
Dit betekent dat met de temperatuurstijging het volume zal toenemen; bij afnemende temperatuur neemt het volume af. In zijn experiment berekende hij dat het volume van een bepaalde massa van een gas met 1/273,15 keer het oorspronkelijke volume toeneemt of afneemt met respectievelijk elke graad stijging of daling van de temperatuur.
Daarom, als het volume V 0 is bij 0 O C en V t het volume is bij t o C dan,
\(V_t = V_0 + \frac{t}{273.15} V_0\)
Hier is de grafische weergave van de wet van Charles:
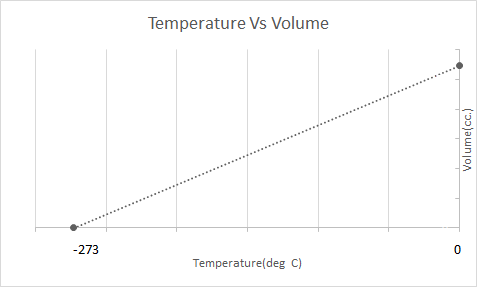
Heteluchtballonnen werken op basis van de wet van Charles. Wanneer een brander de lucht in de ballon verwarmt, beginnen de luchtmoleculen sneller te bewegen en zetten ze uit. Het gas in de ballon neemt meer ruimte in beslag en wordt minder dicht dan de lucht eromheen. Naarmate de heteluchtballon minder dicht wordt, stijgt hij op en blijft hij drijven.
Dit wordt ook wel de Drukwet genoemd. Het werd geformuleerd door Joseph Louis Gay-Lussac in 1808.
De wet van Gay Lussac stelt dat bij constant volume de druk van een ideaal gas recht evenredig is met de absolute temperatuur (in Kelvin).
\(P ∝ T\)
\(P/T = k \)
waar
De wet van Gay-Lussac kan worden uitgedrukt als:
\(\frac{P_1}{T_1} = \frac{P_2}{T_2}\)
Waar:
Volgens de wet van Gay-Lussac neemt de druk van een gas (op constant volume gehouden) constant af naarmate het wordt afgekoeld totdat het gas uiteindelijk condenseert en een vloeistof wordt.
Hier is de grafische weergave van de wet van Gay-Lussac
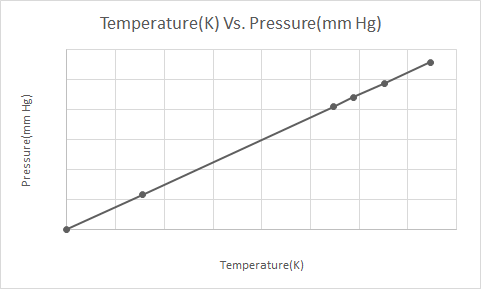
Wanneer een spuitbus onder druk (bijv. deodorantbus of verfspuitbus) wordt verwarmd, kan de resulterende toename van de druk die door de gassen op de container wordt uitgeoefend, leiden tot een explosie. Dit is de reden waarom veel containers onder druk waarschuwingslabels hebben die aangeven dat de container uit de buurt van vuur moet worden gehouden en in een koele omgeving moet worden bewaard.
Wanneer een snelkookpan wordt verwarmd, neemt de druk die wordt uitgeoefend door de stoom in de container toe. De hoge temperatuur en druk in de container zorgen ervoor dat het voedsel sneller gaart.