يعتمد كلا جزئي حساب التفاضل والتكامل، حساب التفاضل والتكامل، على الحدود .
الحد هو أفضل توقع لنقطة ما. فهو يُعطينا تقديرًا عندما لا نستطيع حساب النتيجة مباشرةً. الحد هو القيمة التي تقترب منها الدالة عند اقتراب المُدخل من قيمة معينة.
دعونا نفهم هذا المفهوم باستخدام مثال.
دع f(x) = 4x − 3. احسب قيم f(x) عندما تقترب قيمة x من 3. انظر إلى الرسم البياني للدالة f(x) = 4x − 3. افحص النقاط التي تكون فيها x أقرب إلى 3.
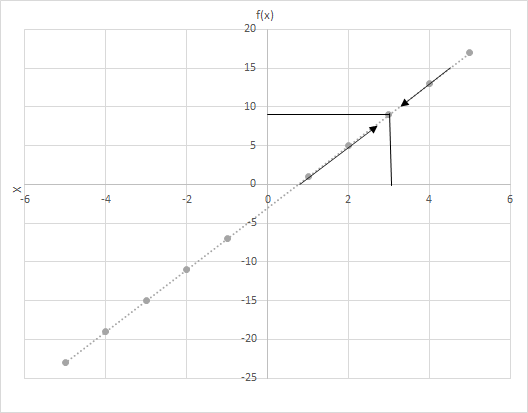
خذ بعين الاعتبار سيناريوهين هنا
(i) x تقترب من 3 من اليسار و
(ii) x تقترب من 3 من اليمين.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3.5 | 11 | |
| 2.5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3.12 | 9.48 | |
| 2.9 | 8.6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3.09 | 9.36 | |
| 2.95 | 8.8 | 3.05 | 9.2 | |
| 2.999 | 8.996 | 3.01 | 9.04 |
هل ترى الصف الأخير؟ في كلتا الحالتين، عندما تقترب x من 3، تقترب f(x) من 9. لذلك، يمكننا القول:
\(\lim\limits_{x \to 3} f(x) = 9\)
لنأخذ مثالًا آخر، نجد الحد الأقصى للدالة f(x) عندما تقترب x من 2، حيث \(f(x) = \frac{x^2 - 4}{x-2}\) ، أي \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
إذا وضعنا قيمة x على أنها 2 نحصل على: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{غير محدد}\)
هذا يعني أنه لا يمكننا الحصول على قيمة الحد باستبدال قيمة x في التعبير. لنحسب قيمة f(x) عندما تقترب x من 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.99 | 3.99 |
عندما يقترب x من 2، تقترب قيمة \(f(x) = \frac{x^2 - 4}{x-2}\) من 4. لذلك،
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
يمكن تعريف الاستمرارية مفاهيميًا بعدة طرق مختلفة. تُعتبر الدالة متصلة إذا أمكن رسم رسمها البياني بقلم دون رفع القلم عن الصفحة. وتُعتبر متصلة إذا كان رسمها البياني منحنىً غير منقطع، دون فجوات أو فواصل. تُمثل الرسوم البيانية أدناه دوالًا متصلة.
كتعريف أكثر رسمية للاستمرارية، يمكننا القول أن الدالة f(x) مستمرة عند النقطة x = a إذا تم استيفاء الشروط التالية:
(i) f(a) مُعرَّفة (ii) \(\lim\limits_{x \to a} f(x) \) موجودة (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
تحقق من الدوال الموضحة في الرسوم البيانية أدناه. كلتا الدالتين لا تستوفيان شروط الاستمرارية الثلاثة:
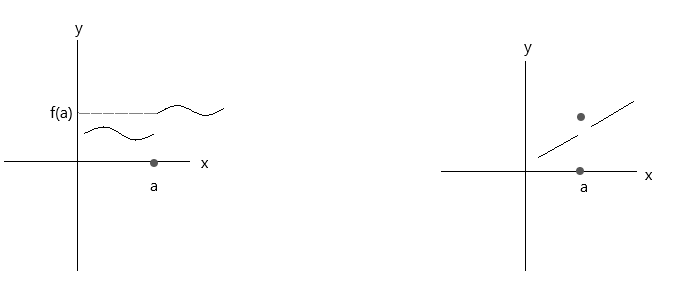
انظر إلى الرسم البياني الأول، \(\lim\limits_{x \to a} f(x) \) = f(a) عند النقطة a تكون صحيحة إذا اقتربت x من القيمة 'a' من الجانب الأيمن. أما إذا اقتربت x من القيمة 'a' من الجانب الأيسر، فإن f(x) لا تقترب من f(a)، وبالتالي فهي دالة غير متصلة.