Hesablamanın hər iki hissəsi, Diferensial və İnteqral hesablamalar Limitlərə əsaslanır.
Limit bir nöqtənin ən yaxşı proqnozudur. Nəticəni birbaşa hesablaya bilmədiyimiz zaman bizə təxmini verir. Limit, girişin bəzi dəyərə "yaxınması" kimi funksiyanın "yaxınlaşdığı" dəyərdir.
Bir nümunədən istifadə edərək bu anlayışı başa düşək.
Qoy f(x) = 4x − 3. X-in 3-ə yaxın dəyər verdiyi üçün f(x)-in qiymətlərini hesablayın. f(x) = 4x − 3 funksiyasının qrafikinə baxın. X-in 3-ə yaxın olduğu nöqtələri araşdırın.
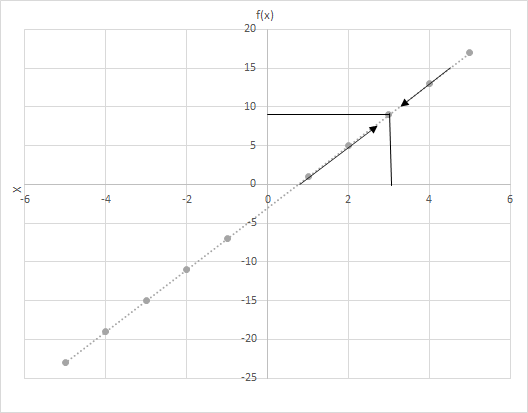
Burada iki ssenarini nəzərdən keçirək
(i) x soldan 3-ə yaxınlaşır və
(ii) x sağdan 3-ə yaxınlaşır.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3,5 | 11 | |
| 2,5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3,12 | 9,48 | |
| 2,9 | 8,6 | 3,1 | 9,4 | |
| 2,91 | 8,64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3.01 | 9.04 |
Son sıranı görürsən? Hər iki halda x 3-ə yaxınlaşdıqda f(x) 9-a yaxınlaşır. Buna görə də deyə bilərik:
\(\lim\limits_{x \to 3} f(x) = 9\)
Başqa bir misal götürək, x 2-yə yaxınlaşdıqca f(x) funksiyasının limitini tapın, burada \(f(x) = \frac{x^2 - 4}{x-2}\) , yəni \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Əgər x-in qiymətini 2 kimi qoysaq, alarıq: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{müəyyən edilməmiş}\)
Bu o deməkdir ki, ifadədə x-in dəyərini əvəz etməklə limitin qiymətini əldə edə bilməyəcəyik. x 2-yə yaxınlaşdıqca f(x) dəyərini hesablayaq.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,993 | . |
x 2-yə yaxınlaşdıqca \(f(x) = \frac{x^2 - 4}{x-2}\) dəyəri 4-ə yaxınlaşır.
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Davamlılıq konseptual olaraq bir neçə fərqli şəkildə müəyyən edilə bilər. Əgər onun qrafiki qələmi səhifədən qaldırmadan qələmlə izlənilə bilərsə, funksiya davamlıdır. Əgər onun qrafiki heç bir deşik, boşluq və ya qırılma olmayan kəsilməyən əyridirsə, funksiya davamlıdır. Aşağıdakı qrafiklər davamlı funksiyaları təmsil edir.
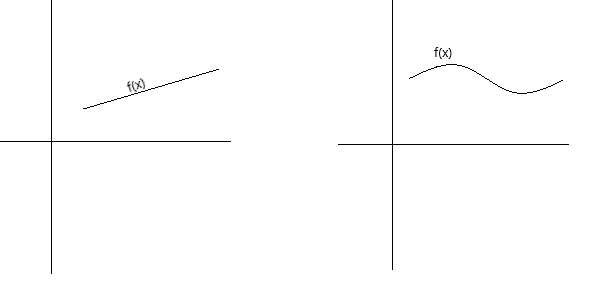
Davamlılığın daha formal tərifi olaraq, aşağıdakı şərtlər yerinə yetirildikdə f(x) funksiyasının x = a nöqtəsində fasiləsiz olduğunu deyə bilərik:
(i) f(a) müəyyən edilir (ii) \(\lim\limits_{x \to a} f(x) \) mövcuddur (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Aşağıdakı qrafiklərdə göstərilən funksiyaları yoxlayın. Hər iki funksiya üç davamlılıq şərtini təmin etmir:
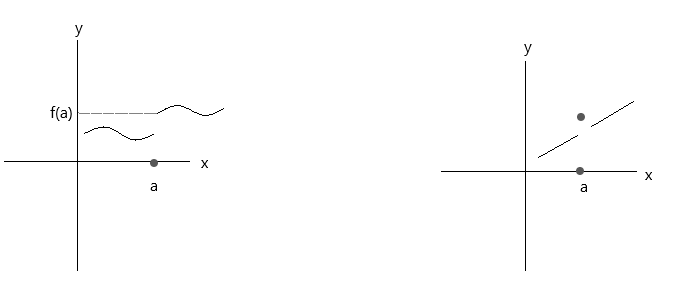
Birinci qrafikə baxın, əgər x 'a' dəyərinə sağ tərəfdən yaxınlaşırsa, a nöqtəsində \(\lim\limits_{x \to a} f(x) \) = f(a) doğrudur. Lakin əgər x 'a' dəyərinə sol tərəfdən yaxınlaşırsa, f(x) f(a)-a yaxınlaşmır, deməli, o, fasiləsiz funksiyadır.