ক্যালকুলাসের উভয় অংশ, ডিফারেনশিয়াল এবং ইন্টিগ্রাল ক্যালকুলাস, লিমিটসের উপর ভিত্তি করে।
সীমা হলো একটি বিন্দুর সর্বোত্তম ভবিষ্যদ্বাণী। যখন আমরা সরাসরি ফলাফল গণনা করতে পারি না তখন এটি আমাদের একটি অনুমান দেয়। সীমা হলো সেই মান যা ফাংশনটি 'পড়তে' পারে যখন ইনপুটটি কোনও মানের 'পড়তে' পারে।
আসুন একটি উদাহরণ ব্যবহার করে এই ধারণাটি বুঝতে পারি।
ধরুন f(x) = 4x − 3। x এর মান 3 এর কাছাকাছি নিয়ে গেলে f(x) এর মান গণনা করুন। f(x) = 4x − 3 ফাংশনের জন্য গ্রাফটি দেখুন। x 3 এর কাছাকাছি কোন বিন্দুতে অবস্থিত তা পরীক্ষা করুন।
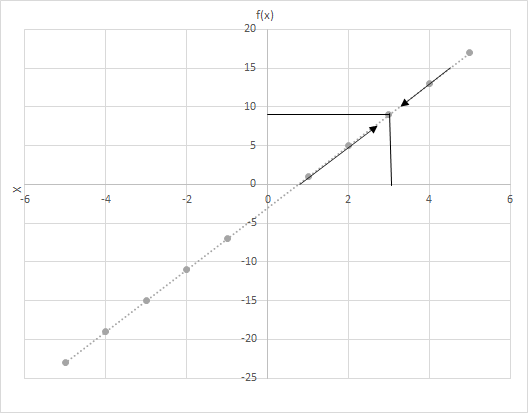
এখানে দুটি পরিস্থিতি বিবেচনা করুন
(i) x বাম দিক থেকে 3 এর দিকে এগিয়ে আসছে এবং
(ii) x ডান দিক থেকে 3 এর কাছাকাছি।
| x | চ(এক্স) | x | চ(এক্স) | |
| ২ | ৫ | ৪ | ১৩ | |
| ২.২ | ৫.৮ | ৩.৫ | ১১ | |
| ২.৫ | ৭ | ৩.২ | ৯.৮ | |
| ২.৮ | ৮.২ | ৩.১২ | ৯.৪৮ | |
| ২.৯ | ৮.৬ | ৩.১ | ৯.৪ | |
| ২.৯১ | ৮.৬৪ | ৩.০৯ | ৯.৩৬ | |
| ২.৯৫ | ৮.৮ | ৩.০৫ | ৯.২ | |
| ২.৯৯৯ | ৮.৯৯৬ | ৩.০১ | ৯.০৪ |
তুমি কি শেষ সারিটি দেখতে পাচ্ছ? উভয় ক্ষেত্রেই x যখন 3 এর কাছাকাছি আসে, f(x) 9 এর কাছাকাছি আসে। অতএব, আমরা বলতে পারি:
\(\lim\limits_{x \to 3} f(x) = 9\)
আরেকটি উদাহরণ দেওয়া যাক, x 2 এর কাছাকাছি পৌঁছানোর সাথে সাথে f(x) ফাংশনের সীমা বের করুন, যেখানে \(f(x) = \frac{x^2 - 4}{x-2}\) , অর্থাৎ \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
যদি আমরা x এর মান 2 হিসেবে রাখি, তাহলে আমরা পাব: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{অনির্ধারিত}\)
এর অর্থ হল, রাশিতে x এর মান প্রতিস্থাপন করে আমরা সীমার মান পেতে পারি না। x 2 এর কাছাকাছি পৌঁছানোর সাথে সাথে f(x) এর মান গণনা করা যাক।
| x | f(x) | x | f(x) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.99 | 3.99 |
x যখন 2 এর কাছাকাছি পৌঁছায়, \(f(x) = \frac{x^2 - 4}{x-2}\) এর মান 4 এর কাছাকাছি পৌঁছায়। অতএব,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
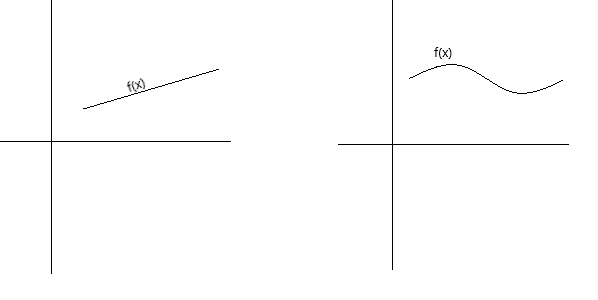
ধারাবাহিকতাকে ধারণাগতভাবে কয়েকটি ভিন্ন উপায়ে সংজ্ঞায়িত করা যেতে পারে। একটি ফাংশন হল অবিচ্ছিন্ন, যদি এর গ্রাফটি পৃষ্ঠা থেকে কলম না তুলে কলম দিয়ে ট্রেস করা যায়। একটি ফাংশন হল অবিচ্ছিন্ন যদি এর গ্রাফটি একটি অখণ্ড বক্ররেখা হয় যার কোনও গর্ত, ফাঁক বা বিরতি নেই। নীচের গ্রাফগুলি অবিচ্ছিন্ন ফাংশনগুলিকে প্রতিনিধিত্ব করে।
ধারাবাহিকতার আরও আনুষ্ঠানিক সংজ্ঞা হিসেবে, আমরা বলতে পারি যে একটি ফাংশন f(x) x = a বিন্দুতে অবিচ্ছিন্ন থাকে যদি নিম্নলিখিত শর্তগুলি পূরণ করা হয়:
(i) f(a) সংজ্ঞায়িত করা হয়েছে (ii) \(\lim\limits_{x \to a} f(x) \) বিদ্যমান (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
নিচের গ্রাফে দেখানো ফাংশনগুলো পরীক্ষা করুন। দুটি ফাংশনই তিনটি ধারাবাহিকতা শর্ত পূরণ করে না:
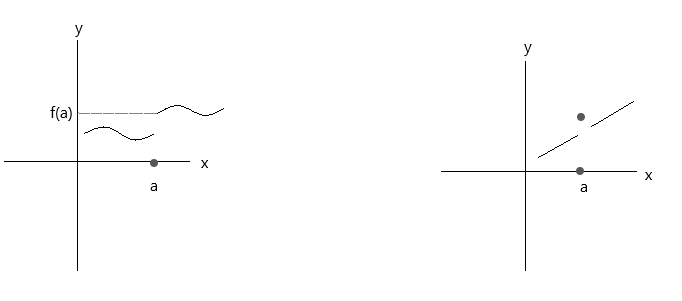
প্রথম গ্রাফটি দেখুন, \(\lim\limits_{x \to a} f(x) \) = f(a) বিন্দু a তে যদি x ডান দিক থেকে 'a' মানের কাছে আসে, তাহলে সত্য হবে। কিন্তু যদি x বাম দিক থেকে 'a' মানের কাছে আসে, তাহলে f(x) f(a) এর কাছে আসছে না, তাই এটি একটি বিচ্ছিন্ন ফাংশন।