Beide Teile der Differential- und Integralrechnung basieren auf Grenzwerten .
Der Grenzwert ist die beste Vorhersage eines Punktes. Er liefert uns eine Schätzung, wenn wir das Ergebnis nicht direkt berechnen können. Der Grenzwert ist der Wert, dem sich die Funktion annähert, wenn sich die Eingabe einem bestimmten Wert annähert.
Lassen Sie uns dieses Konzept anhand eines Beispiels verstehen.
Sei f(x) = 4x − 3. Berechnen Sie die Werte von f(x), wenn x einen Wert annimmt, der sich 3 annähert. Sehen Sie sich die Grafik für die Funktion f(x) = 4x − 3 an. Untersuchen Sie die Punkte, an denen x näher an 3 liegt.
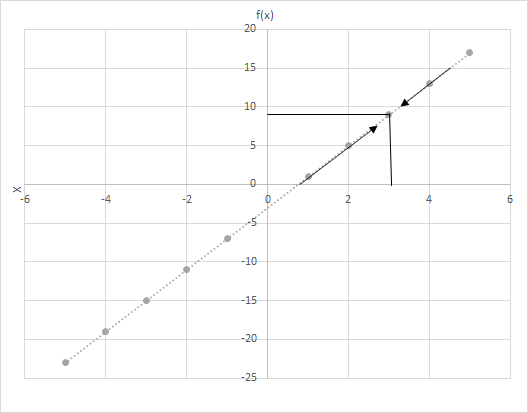
Betrachten Sie hier zwei Szenarien
(i) x nähert sich 3 von links und
(ii) x nähert sich 3 von rechts.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2,2 | 5,8 | 3,5 | 11 | |
| 2,5 | 7 | 3,2 | 9,8 | |
| 2,8 | 8,2 | 3,12 | 9,48 | |
| 2,9 | 8,6 | 3,1 | 9,4 | |
| 2,91 | 8,64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3.01 | 9.04 |
Sehen Sie die letzte Zeile? In beiden Fällen nähert sich x dem Wert 3, und f(x) dem Wert 9. Daher können wir sagen:
\(\lim\limits_{x \to 3} f(x) = 9\)
Nehmen wir ein anderes Beispiel: Finden Sie den Grenzwert für die Funktion f(x), wenn x sich 2 nähert, wobei \(f(x) = \frac{x^2 - 4}{x-2}\) , \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Wenn wir den Wert von x als 2 setzen, erhalten wir: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{undefiniert}\)
Dies bedeutet, dass wir den Grenzwert nicht durch Einsetzen des x-Werts im Ausdruck erhalten können. Berechnen wir den Wert von f(x), wenn x sich 2 nähert.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
Wenn x sich 2 nähert, nähert sich der Wert von \(f(x) = \frac{x^2 - 4}{x-2}\) 4. Daher gilt:
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Kontinuität kann konzeptionell auf verschiedene Weise definiert werden. Eine Funktion ist kontinuierlich, wenn ihr Graph mit einem Stift nachgezeichnet werden kann, ohne den Stift vom Blatt abzusetzen. Eine Funktion ist kontinuierlich, wenn ihr Graph eine ununterbrochene Kurve ohne Löcher, Lücken oder Brüche ist. Die folgenden Graphen stellen kontinuierliche Funktionen dar.
Als formalere Definition der Kontinuität können wir sagen, dass eine Funktion f(x) an einem Punkt x = a kontinuierlich ist, wenn die folgenden Bedingungen erfüllt sind:
(i) f(a) ist definiert (ii) \(\lim\limits_{x \to a} f(x) \) existiert (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Überprüfen Sie die in den folgenden Diagrammen dargestellten Funktionen. Beide Funktionen erfüllen die drei Kontinuitätsbedingungen nicht:
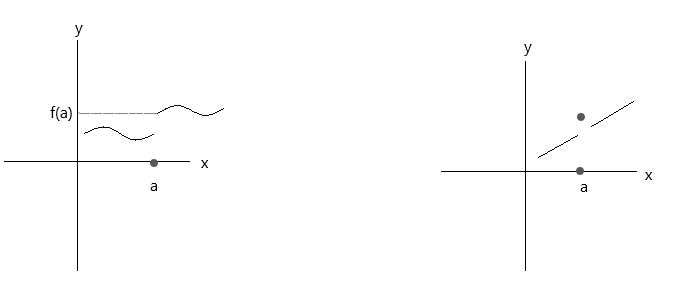
Betrachten Sie die erste Grafik. \(\lim\limits_{x \to a} f(x) \) = f(a) am Punkt a ist wahr, wenn sich x dem Wert 'a' von rechts nähert. Nähert sich x dem Wert 'a' jedoch von links, nähert sich f(x) nicht f(a), es handelt sich also um eine unstetige Funktion.