Both parts of calculus, Differential and Integral calculus are based on Limits.
Limit is the best prediction of a point. It gives us an estimate when we can't compute the result directly. Limit is the value that the function 'approaches' as the input 'approaches' some value.
Let's understand this concept using an example.
Let f(x) = 4x − 3. Compute values of f(x) as x takes value closer to 3. Look at the graph for function f(x) = 4x − 3. Examine points where x is closer to 3.
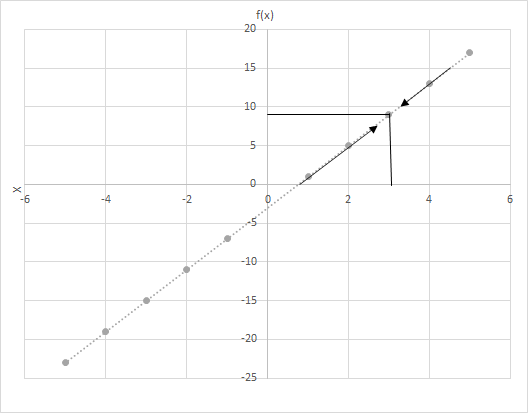
Consider two scenarios here
(i) x approaching 3 from left and
(ii) x approaching 3 from right.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3.5 | 11 | |
| 2.5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3.12 |
9.48 |
|
| 2.9 | 8.6 | 3.1 |
9.4 |
|
| 2.91 | 8.64 | 3.09 | 9.36 | |
| 2.95 | 8.8 | 3.05 | 9.2 | |
| 2.999 | 8.996 | 3.01 | 9.04 |
Do you see the last row? In both the cases as x approaches 3, f(x) approaches 9. Therefore, we can say:
\(\lim\limits_{x \to 3} f(x) = 9\)
Let's take another example, find the limit for function f(x) as x approaches 2, where \(f(x) = \frac{x^2 - 4}{x-2}\) , i.e. \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
If we put the value of x as 2 we get: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{undefined}\)
This implies that we can't get the value of limit by substituting value of x in the expression. Let's compute value of f(x) as x approaches 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.99 | 3.99 |
As x approaches 2, value of \(f(x) = \frac{x^2 - 4}{x-2}\) approaches 4. Therefore,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
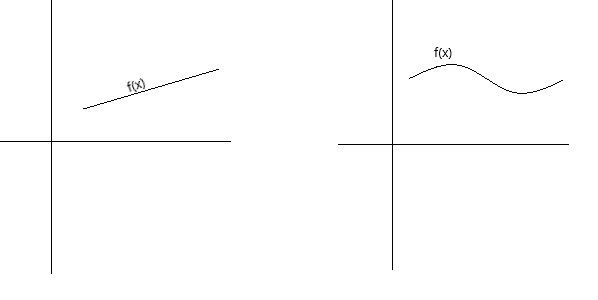
Continuity can be defined conceptually in a few different ways. A function is continuous, if its graph can be traced with a pen without lifting the pen from the page. A function is continuous if its graph is an unbroken curve with no holes, gaps, or breaks. Below graphs represent continuous functions.
As more formal definition of continuity, we can say a function f(x) is continuous at a point x = a if following conditions are met:
(i) f(a) is defined (ii) \(\lim\limits_{x \to a} f(x) \) exists (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Check functions plotted in the graphs below. Both the functions do not satisfy the three continuity conditions:
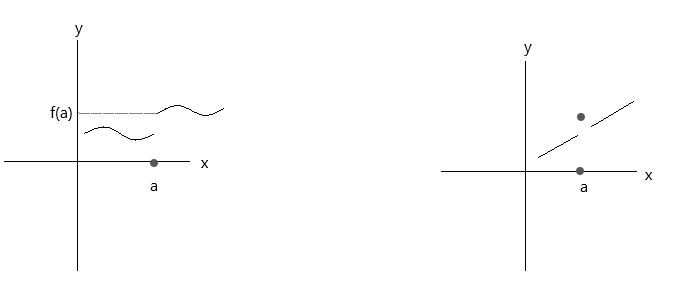
Look at the first graph, \(\lim\limits_{x \to a} f(x) \) = f(a) at point a is true if x approaches value 'a' from the right side. But if x approaches value 'a' from the left side, f(x) is not approaching f(a), hence it is a discontinuous function.