Ambas partes del cálculo, el cálculo diferencial y el cálculo integral, se basan en límites .
El límite es la mejor predicción de un punto. Nos proporciona una estimación cuando no podemos calcular el resultado directamente. El límite es el valor al que la función se aproxima cuando la entrada se aproxima a un valor determinado.
Entendamos este concepto usando un ejemplo.
Sea f(x) = 4x − 3. Calcule los valores de f(x) a medida que x toma un valor más cercano a 3. Observe el gráfico de la función f(x) = 4x − 3. Examine los puntos donde x está más cerca de 3.
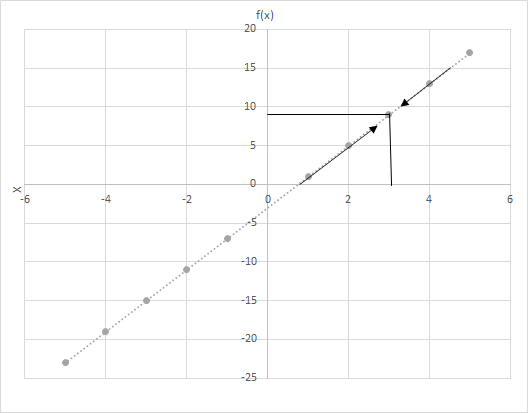
Consideremos dos escenarios aquí
(i) x se acerca a 3 desde la izquierda y
(ii) x se acerca a 3 desde la derecha.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3.5 | 11 | |
| 2.5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3,12 | 9,48 | |
| 2,9 | 8,6 | 3,1 | 9,4 | |
| 2,91 | 8,64 | 3.09 | 9.36 | |
| 2.95 | 8.8 | 3.05 | 9.2 | |
| 2.999 | 8.996 | 3.01 | 9.04 |
¿Ves la última fila? En ambos casos, cuando x tiende a 3, f(x) tiende a 9. Por lo tanto, podemos decir:
\(\lim\limits_{x \to 3} f(x) = 9\)
Tomemos otro ejemplo, busquemos el límite de la función f(x) cuando x tiende a 2, donde \(f(x) = \frac{x^2 - 4}{x-2}\) , es decir, \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Si ponemos el valor de x como 2 obtenemos: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{indefinido}\)
Esto implica que no podemos obtener el valor del límite sustituyendo el valor de x en la expresión. Calculemos el valor de f(x) cuando x tiende a 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.99 | 3.99 |
A medida que x se acerca a 2, el valor de \(f(x) = \frac{x^2 - 4}{x-2}\) se acerca a 4. Por lo tanto,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
La continuidad se puede definir conceptualmente de diferentes maneras. Una función es continua si su gráfica se puede trazar con un bolígrafo sin levantarlo de la página. Una función es continua si su gráfica es una curva continua sin huecos, espacios ni interrupciones. Las siguientes gráficas representan funciones continuas.
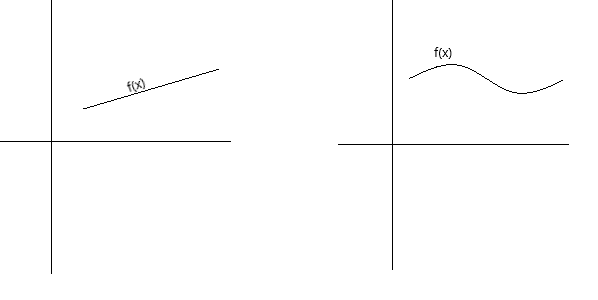
Como definición más formal de continuidad, podemos decir que una función f(x) es continua en un punto x = a si se cumplen las siguientes condiciones:
(i) f(a) está definida (ii) \(\lim\limits_{x \to a} f(x) \) existe (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Verifique las funciones representadas en los gráficos a continuación. Ninguna de las dos funciones cumple las tres condiciones de continuidad:
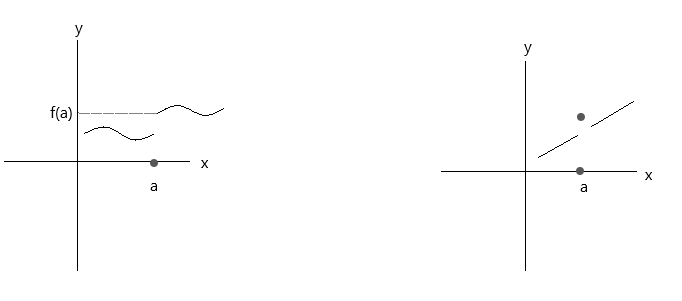
Observa el primer gráfico: \(\lim\limits_{x \to a} f(x) \) = f(a) en el punto a es cierto si x tiende al valor 'a' por el lado derecho. Pero si x tiende al valor 'a' por el lado izquierdo, f(x) no tiende a f(a); por lo tanto, es una función discontinua.