هر دو بخش حساب دیفرانسیل و انتگرال، یعنی حساب دیفرانسیل و انتگرال، بر اساس حدها بنا شدهاند.
حد، بهترین پیشبینی یک نقطه است. وقتی نمیتوانیم نتیجه را مستقیماً محاسبه کنیم، تخمینی به ما میدهد. حد، مقداری است که تابع با نزدیک شدن ورودی به مقداری خاص، به آن نزدیک میشود.
بیایید این مفهوم را با استفاده از یک مثال درک کنیم.
فرض کنید f(x) = 4x−3 باشد. مقادیر f(x) را هنگامی که x به 3 نزدیکتر میشود، محاسبه کنید. به نمودار تابع f(x) = 4x−3 نگاه کنید. نقاطی را که x در آنها به 3 نزدیکتر است، بررسی کنید.
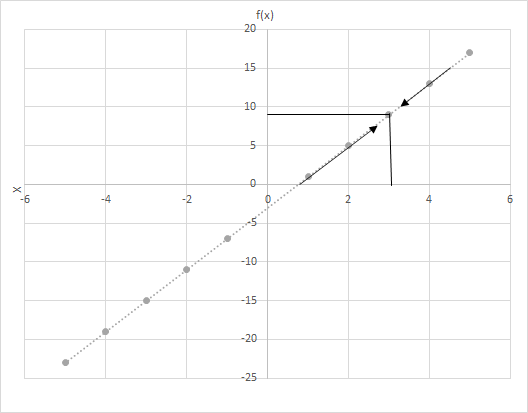
دو حالت را در اینجا در نظر بگیرید
(۱) x از چپ به ۳ نزدیک میشود و
(ii) x از سمت راست به عدد 3 نزدیک میشود.
| ایکس | اف(ایکس) | ایکس | اف(ایکس) | |
| ۲ | ۵ | ۴ | ۱۳ | |
| ۲.۲ | ۵.۸ | ۳.۵ | ۱۱ | |
| ۲.۵ | ۷ | ۳.۲ | ۹.۸ | |
| ۲.۸ | ۸.۲ | ۳.۱۲ | ۹.۴۸ | |
| ۲.۹ | ۸.۶ | ۳.۱ | ۹.۴ | |
| ۲.۹۱ | ۸.۶۴ | ۳.۰۹ | ۹.۳۶ | |
| ۲.۹۵ | ۸.۸ | ۳.۰۵ | ۹.۲ | |
| ۲.۹۹۹ | ۸.۹۹۶ | ۳.۰۱ | ۹.۰۴ |
ردیف آخر را میبینید؟ در هر دو مورد، وقتی x به ۳ نزدیک میشود، f(x) به ۹ نزدیک میشود. بنابراین، میتوانیم بگوییم:
\(\lim\limits_{x \to 3} f(x) = 9\)
بیایید مثال دیگری بزنیم، حد تابع f(x) را هنگامی که x به 2 نزدیک میشود، پیدا کنید، که در آن \(f(x) = \frac{x^2 - 4}{x-2}\) ، یعنی \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
اگر مقدار x را برابر با ۲ قرار دهیم، خواهیم داشت: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{تعریف نشده}\)
این نشان میدهد که نمیتوانیم مقدار حد را با جایگزینی مقدار x در عبارت بدست آوریم. بیایید مقدار f(x) را با میل x به ۲ محاسبه کنیم.
| x | f(x) | x | f(x) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.99 | 3.99 |
همانطور که x به ۲ نزدیک میشود، مقدار \(f(x) = \frac{x^2 - 4}{x-2}\) به ۴ نزدیک میشود. بنابراین،
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
پیوستگی را میتوان از نظر مفهومی به چند روش مختلف تعریف کرد. یک تابع پیوسته است، اگر نمودار آن را بتوان با یک خودکار بدون بلند کردن خودکار از روی صفحه رسم کرد. یک تابع پیوسته است اگر نمودار آن یک منحنی بدون شکست و بدون سوراخ، شکاف یا شکستگی باشد. نمودارهای زیر توابع پیوسته را نشان میدهند.
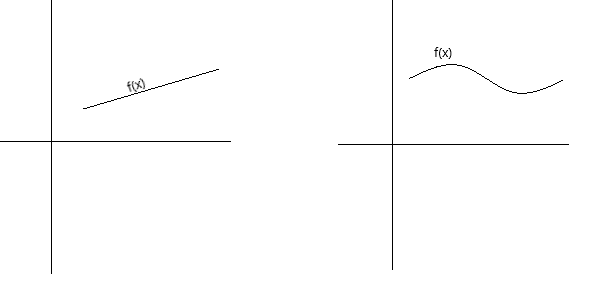
به عنوان تعریف رسمیتر پیوستگی، میتوانیم بگوییم که تابع f(x) در نقطه x = a پیوسته است اگر شرایط زیر برقرار باشد:
(i) تابع f(a) تعریف میشود (ii) \(\lim\limits_{x \to a} f(x) \) وجود دارد (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
توابع رسم شده در نمودارهای زیر را بررسی کنید. هر دو تابع، سه شرط پیوستگی را برآورده نمیکنند:
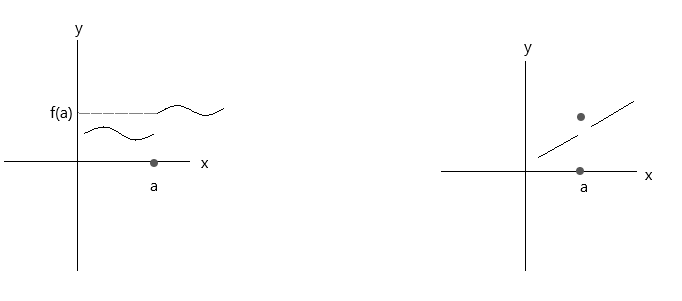
به نمودار اول نگاه کنید، \(\lim\limits_{x \to a} f(x) \) = f(a) در نقطه a درست است اگر x از سمت راست به مقدار 'a' نزدیک شود. اما اگر x از سمت چپ به مقدار 'a' نزدیک شود، f(x) به f(a) نزدیک نمیشود، از این رو یک تابع ناپیوسته است.