Les deux parties du calcul, le calcul différentiel et le calcul intégral, sont basées sur les limites .
La limite est la meilleure prédiction d'un point. Elle nous donne une estimation lorsque nous ne pouvons pas calculer le résultat directement. La limite est la valeur que la fonction « approche » lorsque l'entrée « approche » une valeur donnée.
Comprenons ce concept à l’aide d’un exemple.
Soit f(x) = 4x − 3. Calculez les valeurs de f(x) lorsque x se rapproche de 3. Regardez le graphique de la fonction f(x) = 4x − 3. Examinez les points où x est plus proche de 3.
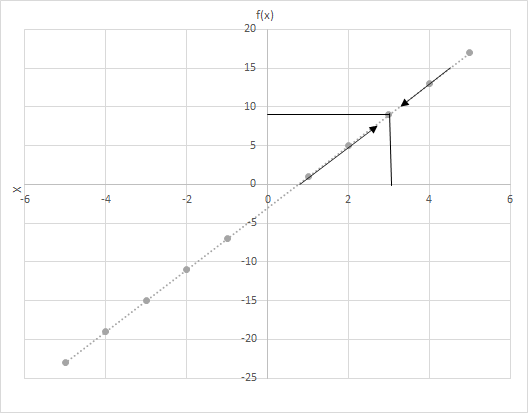
Considérons ici deux scénarios
(i) x approchant 3 depuis la gauche et
(ii) x approchant 3 depuis la droite.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2,2 | 5,8 | 3,5 | 11 | |
| 2,5 | 7 | 3,2 | 9,8 | |
| 2,8 | 8,2 | 3,12 | 9,48 | |
| 2,9 | 8,6 | 3,1 | 9,4 | |
| 2,91 | 8,64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3.01 | 9.04 |
Voyez-vous la dernière ligne ? Dans les deux cas, lorsque x tend vers 3, f(x) tend vers 9. On peut donc dire :
\(\lim\limits_{x \to 3} f(x) = 9\)
Prenons un autre exemple, trouvons la limite de la fonction f(x) lorsque x approche 2, où \(f(x) = \frac{x^2 - 4}{x-2}\) , c'est \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Si nous mettons la valeur de x à 2, nous obtenons : \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{indéfini}\)
Cela implique que nous ne pouvons pas obtenir la valeur de la limite en remplaçant la valeur de x dans l'expression. Calculons la valeur de f(x) lorsque x tend vers 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
Lorsque x approche 2, la valeur de \(f(x) = \frac{x^2 - 4}{x-2}\) approche 4. Par conséquent,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
La continuité peut être définie conceptuellement de différentes manières. Une fonction est continue si son graphique peut être tracé au stylo sans lever le stylo de la page. Une fonction est continue si son graphique est une courbe continue, sans trous, ni interruptions. Les graphiques ci-dessous représentent des fonctions continues.
Comme définition plus formelle de la continuité, nous pouvons dire qu'une fonction f(x) est continue en un point x = a si les conditions suivantes sont remplies :
(i) f(a) est défini (ii) \(\lim\limits_{x \to a} f(x) \) existe (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Vérifiez les fonctions représentées dans les graphiques ci-dessous. Aucune de ces fonctions ne satisfait aux trois conditions de continuité :
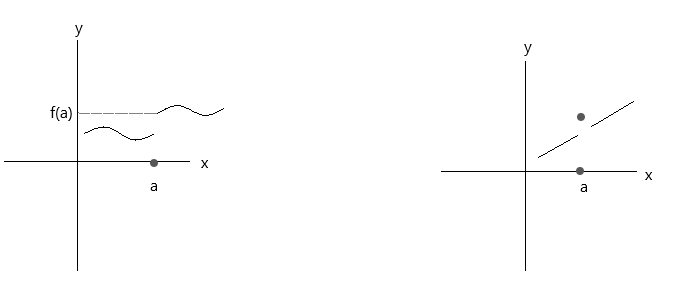
Regardons le premier graphique : \(\lim\limits_{x \to a} f(x) \) = f(a) au point a est vraie si x approche la valeur « a » par la droite. Mais si x approche la valeur « a » par la gauche, f(x) n'approche pas f(a), c'est donc une fonction discontinue.