कलन के दोनों भाग, विभेदक और समाकलन कलन सीमा पर आधारित हैं।
सीमा किसी बिंदु का सबसे अच्छा पूर्वानुमान है। यह हमें एक अनुमान देता है जब हम सीधे परिणाम की गणना नहीं कर सकते। सीमा वह मान है जिस तक फ़ंक्शन 'पहुँचता है' जब इनपुट किसी मान के 'पहुँचता है'।
आइये एक उदाहरण का उपयोग करके इस अवधारणा को समझें।
मान लीजिए f(x) = 4x − 3. f(x) के मान की गणना करें क्योंकि x का मान 3 के करीब है। फ़ंक्शन f(x) = 4x − 3 के लिए ग्राफ़ देखें। उन बिंदुओं की जाँच करें जहाँ x 3 के करीब है।
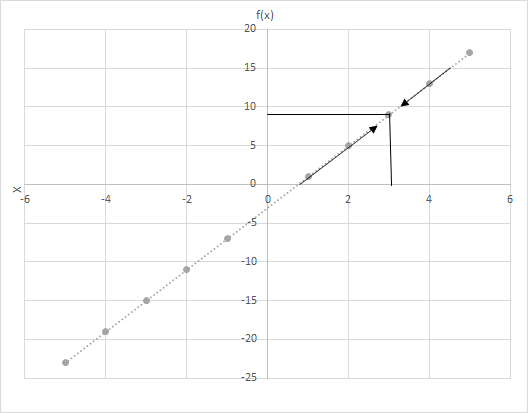
यहां दो परिदृश्यों पर विचार करें
(i) x बायीं ओर से 3 की ओर बढ़ रहा है और
(ii) x दाईं ओर से 3 की ओर बढ़ रहा है।
| एक्स | एफ(एक्स) | एक्स | एफ(एक्स) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3.5 | 11 | |
| 2.5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3.12 | 9.48 | |
| 2.9 | 8.6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3.09 | 9.36 | |
| 2.95 | 8.8 | 3.05 | 9.2 | |
| 2.999 | 8.996 | 3.01 | 9.04 |
क्या आप अंतिम पंक्ति देख रहे हैं? दोनों मामलों में जैसे-जैसे x 3 के करीब पहुंचता है, f(x) 9 के करीब पहुंचता है। इसलिए, हम कह सकते हैं:
\(\lim\limits_{x \to 3} f(x) = 9\)
आइए एक और उदाहरण लेते हैं, फ़ंक्शन f(x) के लिए सीमा ज्ञात करें जैसे ही x 2 के निकट पहुंचता है, जहाँ \(f(x) = \frac{x^2 - 4}{x-2}\) , यानी \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
यदि हम x का मान 2 रखें तो हमें प्राप्त होता है: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{अपरिभाषित}\)
इसका तात्पर्य यह है कि हम अभिव्यक्ति में x का मान प्रतिस्थापित करके सीमा का मान प्राप्त नहीं कर सकते। आइए x के 2 के निकट पहुँचने पर f(x) का मान परिकलित करें।
| एक्स | एफ(एक्स) | एक्स | एफ(एक्स) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.99 | 3.99 |
जैसे-जैसे x 2 के करीब पहुंचता है, \(f(x) = \frac{x^2 - 4}{x-2}\) का मान 4 के करीब पहुंचता है। इसलिए,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
निरंतरता को वैचारिक रूप से कुछ अलग तरीकों से परिभाषित किया जा सकता है। एक फ़ंक्शन निरंतर होता है, अगर उसका ग्राफ़ पेज से पेन उठाए बिना पेन से ट्रेस किया जा सकता है। एक फ़ंक्शन निरंतर होता है अगर उसका ग्राफ़ एक अखंडित वक्र है जिसमें कोई छेद, अंतराल या टूटन नहीं है। नीचे दिए गए ग्राफ़ निरंतर फ़ंक्शन को दर्शाते हैं।
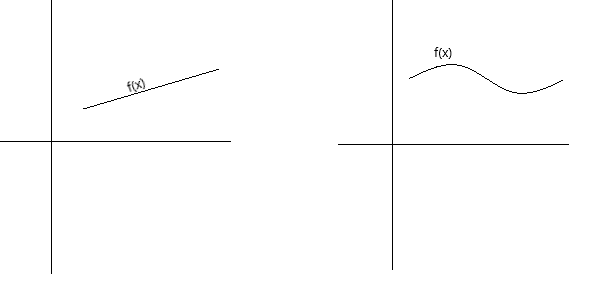
सातत्य की अधिक औपचारिक परिभाषा के रूप में, हम कह सकते हैं कि एक फलन f(x) बिंदु x = a पर सतत है, यदि निम्नलिखित शर्तें पूरी होती हैं:
(i) f(a) परिभाषित है (ii) \(\lim\limits_{x \to a} f(x) \) विद्यमान है (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
नीचे दिए गए ग्राफ़ में दिखाए गए फ़ंक्शन की जाँच करें। दोनों फ़ंक्शन तीन निरंतरता शर्तों को पूरा नहीं करते हैं:
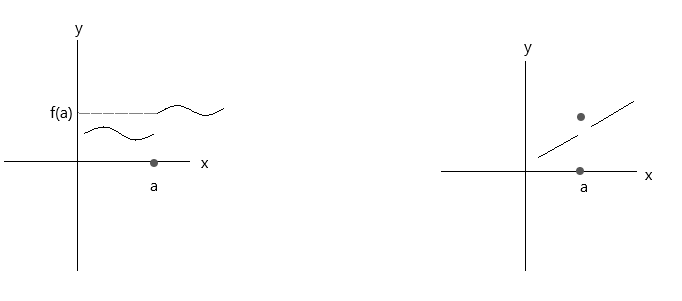
पहले ग्राफ को देखें, \(\lim\limits_{x \to a} f(x) \) = f(a) बिंदु a पर सत्य है यदि x दाईं ओर से मान 'a' के पास पहुँचता है। लेकिन यदि x बाईं ओर से मान 'a' के पास पहुँचता है, तो f(x) f(a) के पास नहीं पहुँच रहा है, इसलिए यह एक असंतत फ़ंक्शन है।