Oba dijela računa, diferencijalni i integralni račun, temelje se na limesima .
Limit je najbolja predikcija točke. Daje nam procjenu kada ne možemo izravno izračunati rezultat. Limit je vrijednost kojoj se funkcija 'približava' kada se ulaz 'približava' nekoj vrijednosti.
Razumijemo ovaj koncept koristeći primjer.
Neka je f(x) = 4x − 3. Izračunajte vrijednosti f(x) kada x poprima vrijednost bližu 3. Pogledajte graf funkcije f(x) = 4x − 3. Ispitajte točke gdje je x bliži 3.
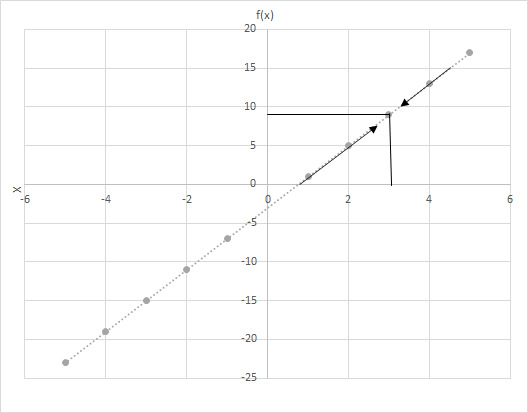
Razmotrite ovdje dva scenarija
(i) x se približava 3 s lijeva i
(ii) x se približava broju 3 s desne strane.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2,2 | 5,8 | 3,5 | 11 | |
| 2,5 | 7 | 3,2 | 9,8 | |
| 2,8 | 8,2 | 3,12 | 9,48 | |
| 2,9 | 8,6 | 3,1 | 9,4 | |
| 2,91 | 8,64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3,01 | 9,04 |
Vidite li zadnji redak? U oba slučaja, kako x teži 3, f(x) teži 9. Stoga možemo reći:
\(\lim\limits_{x \to 3} f(x) = 9\)
Uzmimo još jedan primjer, pronađimo limes funkcije f(x) kada x teži 2, gdje \(f(x) = \frac{x^2 - 4}{x-2}\) , tj \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Ako vrijednost x zapišemo kao 2, dobivamo: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{nedefinirano}\)
To implicira da ne možemo dobiti vrijednost limesa zamjenom vrijednosti x u izrazu. Izračunajmo vrijednost f(x) kada x teži 2.
| x- | f(x) | x- | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
Kako se x približava 2, vrijednost \(f(x) = \frac{x^2 - 4}{x-2}\) približava se 4. Stoga,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Kontinuitet se može konceptualno definirati na nekoliko različitih načina. Funkcija je neprekidna ako se njezin graf može pratiti olovkom bez podizanja olovke sa stranice. Funkcija je neprekidna ako je njezin graf neprekinuta krivulja bez rupa, praznina ili prekida. Donji grafovi predstavljaju neprekidne funkcije.
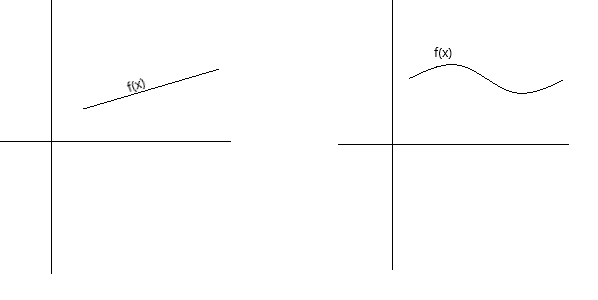
Kao formalnija definicija kontinuiteta, možemo reći da je funkcija f(x) neprekidna u točki x = a ako su ispunjeni sljedeći uvjeti:
(i) f(a) je definirana (ii) \(\lim\limits_{x \to a} f(x) \) postoji (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Provjerite funkcije prikazane na donjim grafovima. Obje funkcije ne zadovoljavaju tri uvjeta kontinuiteta:
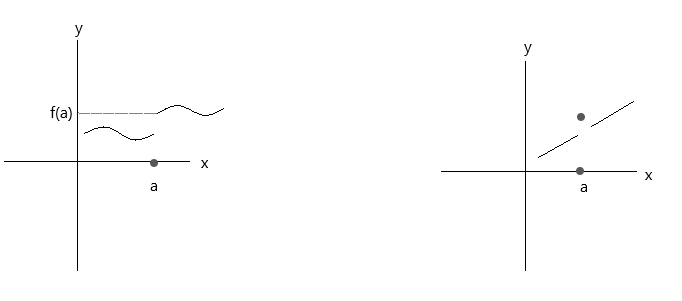
Pogledajte prvi graf, \(\lim\limits_{x \to a} f(x) \) = f(a) u točki a vrijedi ako se x približava vrijednosti 'a' s desne strane. Ali ako se x približava vrijednosti 'a' s lijeve strane, f(x) se ne približava f(a), stoga je to diskontinuirana funkcija.