Kedua bagian kalkulus, Kalkulus Diferensial dan Integral didasarkan pada Limit .
Batas adalah prediksi terbaik dari suatu titik. Batas memberi kita perkiraan ketika kita tidak dapat menghitung hasilnya secara langsung. Batas adalah nilai yang 'didekati' oleh fungsi saat input 'mendekati' suatu nilai.
Mari kita pahami konsep ini menggunakan sebuah contoh.
Misalkan f(x) = 4x − 3. Hitunglah nilai f(x) ketika x mendekati nilai 3. Perhatikan grafik fungsi f(x) = 4x − 3. Periksa titik-titik di mana x mendekati nilai 3.
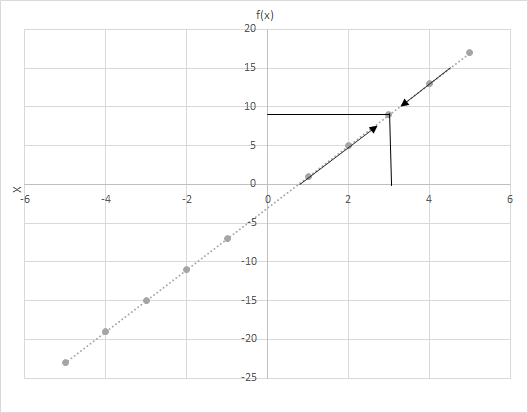
Pertimbangkan dua skenario di sini
(i) x mendekati 3 dari kiri dan
(ii) x mendekati 3 dari kanan.
| x | (x) | xf | (x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3,5 | 11 | |
| 2,5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3.12 | 9.48 | |
| 2.9 | 8.6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3.01 | 9.04 |
Apakah Anda melihat baris terakhir? Dalam kedua kasus tersebut, saat x mendekati 3, f(x) mendekati 9. Oleh karena itu, kita dapat mengatakan:
\(\lim\limits_{x \to 3} f(x) = 9\)
Mari kita ambil contoh lain, cari limit fungsi f(x) saat x mendekati 2, di mana \(f(x) = \frac{x^2 - 4}{x-2}\) , yaitu \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Jika kita meletakkan nilai x sebagai 2 kita memperoleh: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{belum diartikan}\)
Ini berarti kita tidak bisa mendapatkan nilai limit dengan mensubstitusikan nilai x dalam ekspresi tersebut. Mari kita hitung nilai f(x) saat x mendekati 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
Ketika x mendekati 2, nilai \(f(x) = \frac{x^2 - 4}{x-2}\) mendekati 4. Oleh karena itu,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Kontinuitas dapat didefinisikan secara konseptual dalam beberapa cara berbeda. Suatu fungsi bersifat kontinu, jika grafiknya dapat dijiplak dengan pena tanpa mengangkat pena dari halaman. Suatu fungsi bersifat kontinu jika grafiknya berupa kurva tak terputus tanpa lubang, celah, atau putus. Grafik di bawah ini menggambarkan fungsi kontinu.
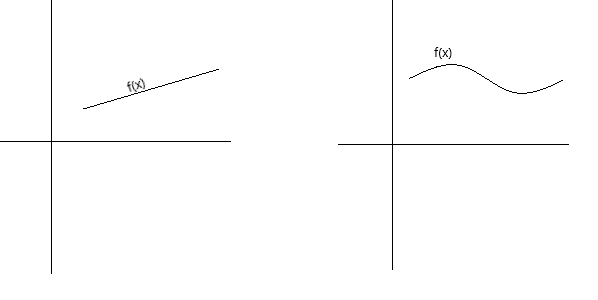
Sebagai definisi formal dari kontinuitas, kita dapat mengatakan suatu fungsi f(x) kontinu pada suatu titik x = a jika kondisi berikut terpenuhi:
(i) f(a) terdefinisi (ii) \(\lim\limits_{x \to a} f(x) \) ada (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Periksa fungsi yang diplot dalam grafik di bawah ini. Kedua fungsi tersebut tidak memenuhi tiga kondisi kontinuitas:
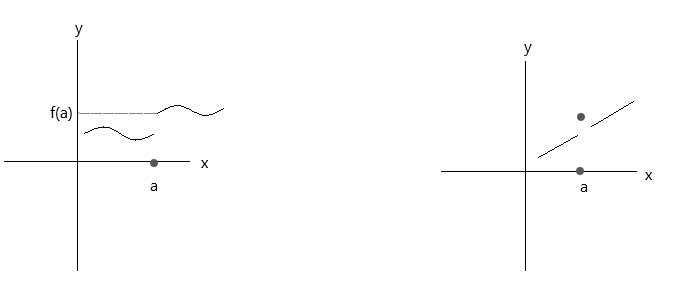
Perhatikan grafik pertama, \(\lim\limits_{x \to a} f(x) \) = f(a) pada titik a berlaku jika x mendekati nilai 'a' dari sisi kanan. Namun jika x mendekati nilai 'a' dari sisi kiri, f(x) tidak mendekati f(a), maka itu adalah fungsi diskontinu.