Entrambe le parti del calcolo differenziale e integrale si basano sui limiti .
Il limite è la migliore previsione di un punto. Ci fornisce una stima quando non possiamo calcolare direttamente il risultato. Il limite è il valore a cui la funzione "si avvicina" quando l'input "si avvicina" a un certo valore.
Cerchiamo di capire meglio questo concetto con un esempio.
Sia f(x) = 4x − 3. Calcola i valori di f(x) quando x assume valori più vicini a 3. Osserva il grafico della funzione f(x) = 4x − 3. Esamina i punti in cui x è più vicino a 3.
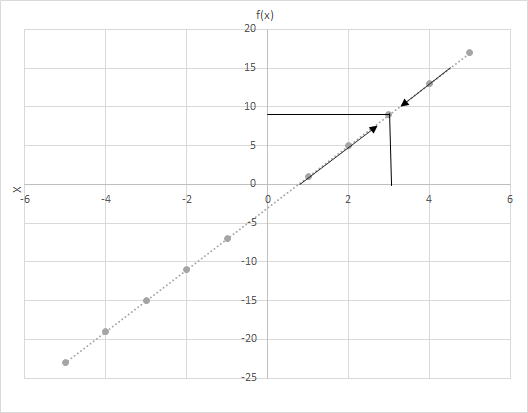
Consideriamo qui due scenari
(i) x che si avvicina a 3 da sinistra e
(ii) x che si avvicina a 3 da destra.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3.5 | 11 | |
| 2.5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3.12 | 9.48 | |
| 2.9 | 8.6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3.01 | 9.04 |
Vedete l'ultima riga? In entrambi i casi, quando x si avvicina a 3, f(x) si avvicina a 9. Pertanto, possiamo dire:
\(\lim\limits_{x \to 3} f(x) = 9\)
Prendiamo un altro esempio: troviamo il limite della funzione f(x) quando x si avvicina a 2, dove \(f(x) = \frac{x^2 - 4}{x-2}\) , ovvero \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Se poniamo il valore di x pari a 2 otteniamo: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{indefinito}\)
Ciò implica che non possiamo ottenere il valore del limite sostituendo il valore di x nell'espressione. Calcoliamo il valore di f(x) quando x tende a 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
Quando x si avvicina a 2, il valore di \(f(x) = \frac{x^2 - 4}{x-2}\) si avvicina a 4. Pertanto,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
La continuità può essere definita concettualmente in diversi modi. Una funzione è continua se il suo grafico può essere tracciato con una penna senza staccarla dal foglio. Una funzione è continua se il suo grafico è una curva continua, senza buchi, interruzioni o interruzioni. I grafici seguenti rappresentano funzioni continue.
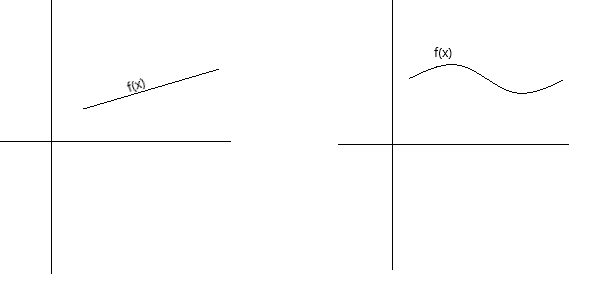
Come definizione più formale di continuità, possiamo dire che una funzione f(x) è continua in un punto x = a se sono soddisfatte le seguenti condizioni:
(i) f(a) è definito (ii) \(\lim\limits_{x \to a} f(x) \) esiste (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Controllare le funzioni rappresentate nei grafici sottostanti. Entrambe le funzioni non soddisfano le tre condizioni di continuità:
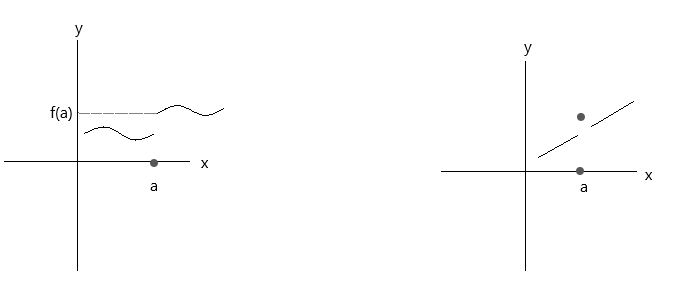
Osservando il primo grafico, \(\lim\limits_{x \to a} f(x) \) = f(a) nel punto a è vero se x si avvicina al valore 'a' da destra. Ma se x si avvicina al valore 'a' da sinistra, f(x) non si avvicina a f(a), quindi è una funzione discontinua.