微積分学の両部分、微分積分学は極限に基づいています。
極限とは、ある点の最良の予測値です。結果を直接計算できない場合に、推定値を与えてくれます。極限とは、入力値がある値に「近づく」ときに関数が「近づく」値です。
例を使ってこの概念を理解してみましょう。
f(x) = 4x − 3 とします。x の値が 3 に近づくにつれて f(x) の値を計算します。関数 f(x) = 4x − 3 のグラフを見てください。x が 3 に近づく点を調べます。
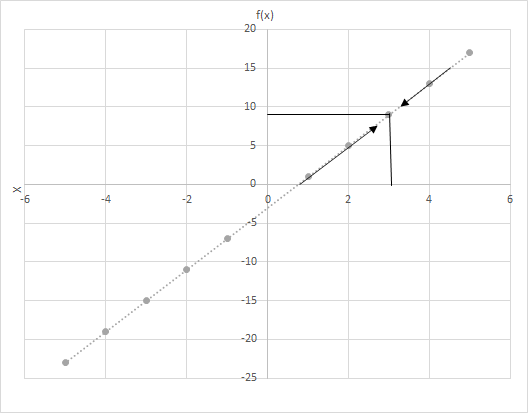
ここで2つのシナリオを考えてみましょう
(i) 左から3番目に近づくxと
(ii) 右から3番目に近づくx。
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3.5 | 11 | |
| 2.5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3.12 | 9.48 | |
| 2.9 | 8.6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3.09 | 9.36 | |
| 2.95 | 8.8 | 3.05 | 9.2 | |
| 2.999 | 8.996 | 3.01 | 9.04 |
最後の行を見てください。どちらの場合も、xが3に近づくにつれて、f(x)は9に近づきます。したがって、次のことが言えます。
\(\lim\limits_{x \to 3} f(x) = 9\)
別の例として、関数 f(x) の x が 2 に近づくときの極限を見つけてみましょう。 \(f(x) = \frac{x^2 - 4}{x-2}\) 、つまり\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
xの値を2とすると、次のようになります: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{未定義}\)
これは、式にxの値を代入しても極限の値を得られないことを意味します。xが2に近づくにつれてf(x)の値を計算してみましょう。
| x | f(x) | x | f(x) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.99 | 3.99 |
xが2に近づくと、 \(f(x) = \frac{x^2 - 4}{x-2}\)の値は4に近づきます。したがって、
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
連続性は概念的にいくつかの方法で定義できます。関数が連続しているとは、そのグラフがペンを紙から離さずにペンでなぞれる場合です。関数が連続しているとは、グラフが途切れることなく、穴や隙間、切れ目がない曲線である場合です。以下のグラフは連続関数を表しています。
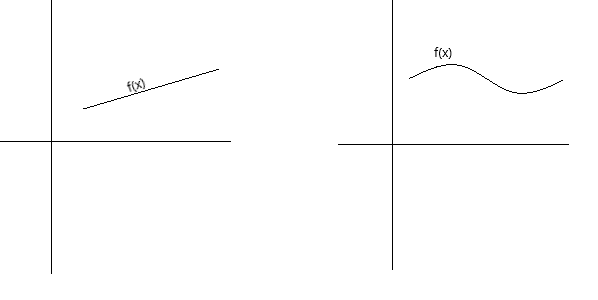
連続性のより正式な定義としては、次の条件が満たされる場合、関数 f(x) は点 x = a で連続していると言えます。
(i) f(a) が定義されている (ii) \(\lim\limits_{x \to a} f(x) \)が存在する (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
下のグラフにプロットされた関数を確認してください。どちらの関数も3つの連続条件を満たしていません。
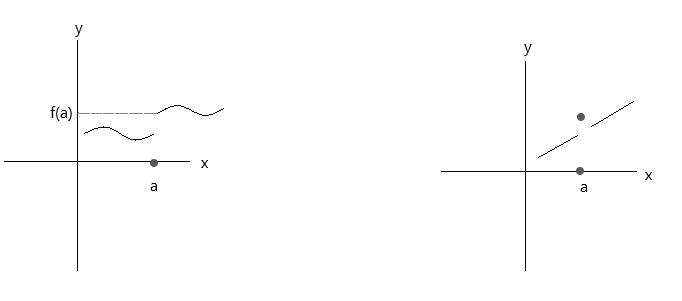
最初のグラフを見てください。点aにおいて、xが右側から値「a」に近づく場合\(\lim\limits_{x \to a} f(x) \) = f(a)が成立します。しかし、xが左側から値「a」に近づく場合、f(x)はf(a)に近づかないため、不連続関数となります。