И двата дела од анализата, диференцијалното и интегралното сметање, се базираат на граници .
Границата е најдоброто предвидување на точка. Ни дава проценка кога не можеме директно да го пресметаме резултатот. Границата е вредноста кон која функцијата „се приближува“ додека влезот „се приближува“ кон некоја вредност.
Да го разбереме овој концепт користејќи пример.
Нека f(x) = 4x − 3. Пресметајте ги вредностите на f(x) како што x ја приближува вредноста до 3. Погледнете го графиконот за функцијата f(x) = 4x − 3. Испитајте ги точките каде што x е поблиску до 3.
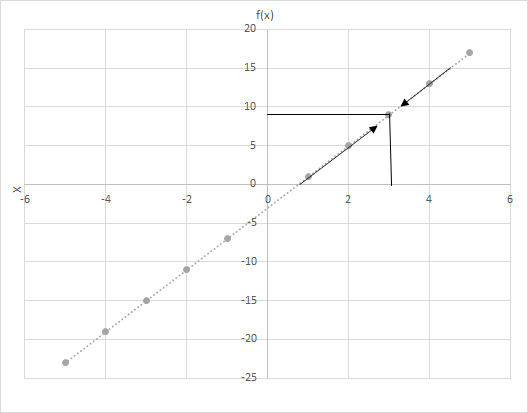
Разгледајте ги двата сценарија овде
(i) x се приближува кон 3 од лево и
(ii) x се приближува кон 3 од десно.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2,2 | 5,8 | 3,5 | 11 | |
| 2,5 | 7 | 3,2 | 9,8 | |
| 2,8 | 8,2 | 3,12 | 9,48 | |
| 2,9 | 8,6 | 3,1 | 9,4 | |
| 2,91 | 8,64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3.01 | 9.04 |
Го гледате ли последниот ред? Во двата случаи, како што x се приближува кон 3, f(x) се приближува кон 9. Затоа, можеме да кажеме:
\(\lim\limits_{x \to 3} f(x) = 9\)
Да земеме друг пример, да ја најдеме границата за функцијата f(x) како што x се приближува кон 2, каде што \(f(x) = \frac{x^2 - 4}{x-2}\) , т.е. \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Ако ја ставиме вредноста на x како 2, добиваме: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{недефиниран}\)
Ова имплицира дека не можеме да ја добиеме вредноста на limit со замена на вредноста на x во изразот. Да ја пресметаме вредноста на f(x) како што x се приближува кон 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
Како што x се приближува кон 2, вредноста на \(f(x) = \frac{x^2 - 4}{x-2}\) се приближува кон 4. Затоа,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Континуитетот може да се дефинира концептуално на неколку различни начини. Функцијата е континуирана ако нејзиниот график може да се исцрта со пенкало без да се крева пенкалото од страницата. Функцијата е континуирана ако нејзиниот график е непрекината крива без дупки, празнини или прекини. Графиконите подолу претставуваат континуирани функции.
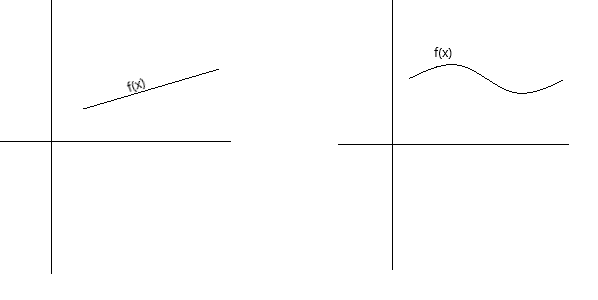
Како поформална дефиниција за континуитет, можеме да кажеме дека функцијата f(x) е континуирана во точка x = a ако се исполнети следните услови:
(i) f(a) е дефинирано (ii) \(\lim\limits_{x \to a} f(x) \) постои (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Проверете ги функциите прикажани на графиконите подолу. Ниту едната ниту другата функција не ги задоволуваат трите услови за континуитет:
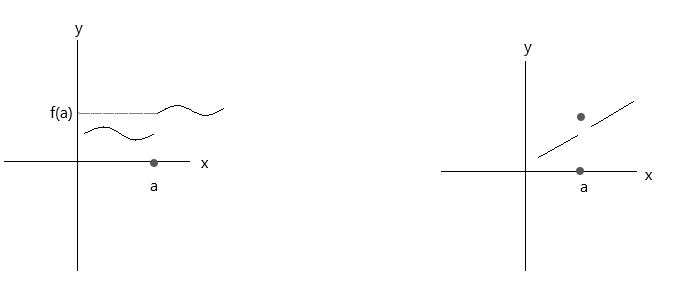
Погледнете го првиот графикон, \(\lim\limits_{x \to a} f(x) \) = f(a) во точката a е точно ако x се приближи до вредноста 'a' од десната страна. Но, ако x се приближи до вредноста 'a' од левата страна, f(x) не се приближува до f(a), па оттука е дисконтинуирана функција.