Тооцооллын хоёр хэсэг, дифференциал ба интеграл тооцоолол нь Хязгаар дээр суурилдаг.
Хязгаар нь цэгийн хамгийн сайн таамаглал юм. Энэ нь үр дүнг шууд тооцоолох боломжгүй үед бидэнд тооцооллыг өгдөг. Хязгаар гэдэг нь оролт нь ямар нэг утгад ойртоход функц "ойртдог" утга юм.
Энэ ойлголтыг жишээ ашиглан ойлгоцгооё.
f(x) = 4x − 3. x нь 3-т ойртож утгыг авч байгаа тул f(x)-ийн утгыг тооцоол. f(x) = 4x − 3 функцийн графикийг харна уу. x нь 3-т ойр байгаа цэгүүдийг шалга.
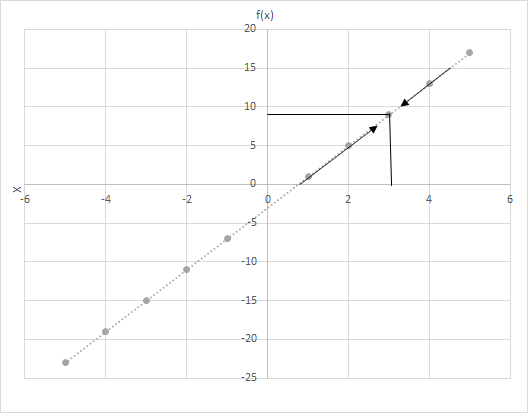
Энд хоёр хувилбарыг авч үзье
(i) зүүнээс 3 руу ойртож буй x ба
(ii) x баруун талаас 3 руу ойртож байна.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3.5 | 11 | |
| 2.5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3.12 | 9.48 | |
| 2.9 | 8.6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3.09 | 9.36 | |
| 2.95 | 8.8 | 3.05 | 9.2 | |
| 2.999 | 8.996 | 3.01 | 9.04 |
Та сүүлчийн эгнээ харж байна уу? Аль ч тохиолдолд x нь 3-т ойртох тусам f(x) 9-д ойртоно. Иймд бид дараахь зүйлийг хэлж болно.
\(\lim\limits_{x \to 3} f(x) = 9\)
Өөр нэг жишээ авч үзье, x 2-т ойртох үед f(x) функцийн хязгаарыг олъё, энд \(f(x) = \frac{x^2 - 4}{x-2}\) , өөрөөр хэлбэл \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Хэрэв бид x-ийн утгыг 2 болговол: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{тодорхойгүй}\)
Энэ нь илэрхийлэл дэх x-ийн утгыг орлуулах замаар бид хязгаарын утгыг авч чадахгүй гэсэн үг юм. x 2-т ойртох үед f(x)-ийн утгыг бодъё.
| х | f(x) | x | f(x) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.993 | . |
x 2-т ойртох тусам \(f(x) = \frac{x^2 - 4}{x-2}\) ийн утга 4-т ойртоно.
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Тасралтгүй байдлыг үзэл баримтлалын хувьд хэд хэдэн янзаар тодорхойлж болно. Функц нь хуудаснаас үзгээ өргөхгүйгээр графыг нь үзэггээр зурж чадвал функц тасралтгүй байна. График нь цоорхой, цоорхой, завсаргүй тасрахгүй муруй байвал функц тасралтгүй байна. Доорх графикууд нь тасралтгүй функцуудыг харуулж байна.
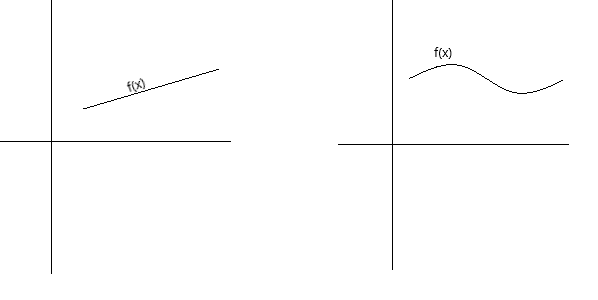
Тасралтгүй байдлын илүү албан ёсны тодорхойлолтын хувьд дараах нөхцөл хангагдсан тохиолдолд f(x) функцийг x = a цэг дээр тасралтгүй гэж хэлж болно.
(i) f(a) тодорхойлогддог (ii) \(\lim\limits_{x \to a} f(x) \) байгаа (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Доорх графикт үзүүлсэн функцуудыг шалгана уу. Энэ хоёр функц нь тасралтгүй байдлын гурван нөхцлийг хангадаггүй:
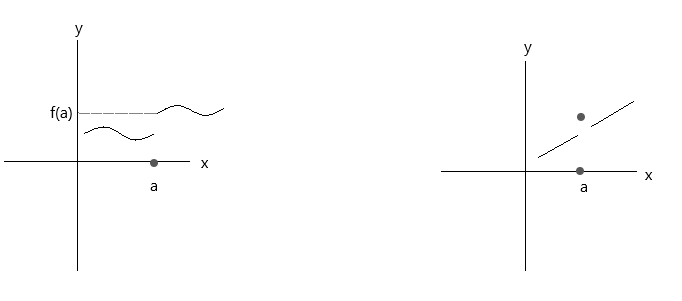
Эхний графикийг харна уу, хэрэв x нь 'a' утгад баруун талаас ойртвол a цэг дэх \(\lim\limits_{x \to a} f(x) \) = f(a) нь үнэн болно. Харин x нь зүүн талаас 'a' утгад ойртвол f(x) нь f(a)-д ойртоогүй тул энэ нь тасархай функц болно.