calculus ၏ အစိတ်အပိုင်း နှစ်ခုစလုံး၊ Differential နှင့် Integral calculus တို့သည် က န့်သတ်ချက်များ အပေါ် အခြေခံသည်။
ကန့်သတ်ချက်သည် အမှတ်တစ်ခု၏ အကောင်းဆုံး ခန့်မှန်းချက်ဖြစ်သည်။ ရလဒ်ကို တိုက်ရိုက်မတွက်ချက်နိုင်သောအခါတွင် ၎င်းသည် ကျွန်ုပ်တို့အား ခန့်မှန်းချက်တစ်ခုပေးသည်။ ကန့်သတ်ချက်သည် လုပ်ဆောင်ချက် 'ချဉ်းကပ်မှု' တွင် ထည့်သွင်းသည့် 'ချဉ်းကပ်မှု' အချို့သော တန်ဖိုးအဖြစ် လုပ်ဆောင်သည့် တန်ဖိုးဖြစ်သည်။
ဥပမာတစ်ခုသုံးပြီး ဒီသဘောတရားကို နားလည်ကြရအောင်။
f(x) = 4x − 3 ဖြစ်ပါစေ။ x သည် 3 နှင့် ပိုနီးစပ်သောကြောင့် f(x) ၏တွက်ချက်မှုတန်ဖိုးများကို တွက်ချက်ပါ။ function f(x) = 4x − 3 အတွက် ဂရပ်ကိုကြည့်ပါ။ x သည် 3 နှင့် ပိုနီးစပ်သည့် အမှတ်များကို ဆန်းစစ်ပါ။
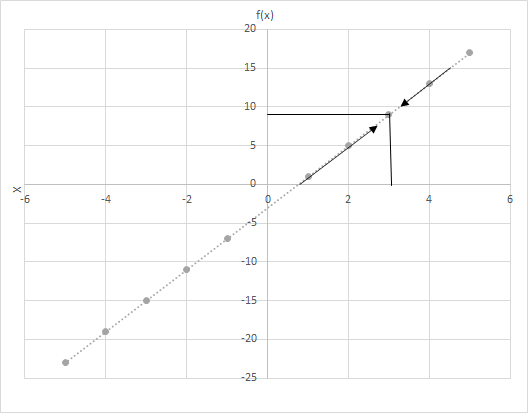
ဤနေရာတွင် မြင်ကွင်းနှစ်ခုကို သုံးသပ်ကြည့်ပါ။
(i) x 3 ကို ဘယ်ဘက်မှ ချဉ်းကပ်၍
(ii) x ညာဘက်မှ 3 သို့ချဉ်းကပ်ခြင်း။
| x | f(x) | x | f(x) | |
| ၂ | ၅ | ၄း | ၁၃ | |
| ၂.၂ | ၅.၈ | ၃.၅ | ၁၁ | |
| ၂.၅ | ၇ | ၃.၂ | ၉.၈ | |
| ၂.၈ | ၈.၂ | ၃.၁၂ | ၉.၄၈ | |
| ၂.၉ | ၈.၆ | ၃.၁ | ၉.၄ | |
| ၂.၉၁ | ၈.၆၄ | ၃.၀၉ | ၉.၃၆ | |
| ၂.၉၅ | ၈.၈ | ၃.၀၅ | ၉.၂ | |
| ၂.၉၉၉ | ၈.၉၉၆ | ၃.၀၁ | ၉.၀၄ |
နောက်ဆုံးအတန်းကိုတွေ့လား။ x ချဉ်းကပ်မှု 3 အဖြစ် ဖြစ်ရပ်နှစ်ခုစလုံးတွင် f(x) သည် 9 သို့ ချဉ်းကပ်သည်။ ထို့ကြောင့်၊
\(\lim\limits_{x \to 3} f(x) = 9\)
နောက်ဥပမာတစ်ခုကိုကြည့်ရအောင်၊ x ချဉ်းကပ်မှု 2 အဖြစ် လုပ်ဆောင်ချက် f(x) အတွက် ကန့်သတ်ချက်ကို ရှာပါ၊ အဲဒီမှာ \(f(x) = \frac{x^2 - 4}{x-2}\) ၊ ဥပမာ \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
x ၏တန်ဖိုးကို 2 အဖြစ်ထည့်လျှင် \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{သတ်မှတ်မထားသော}\)
ဆိုလိုသည်မှာ စကားရပ်တွင် x ၏တန်ဖိုးကို အစားထိုးခြင်းဖြင့် ကန့်သတ်တန်ဖိုးကို ကျွန်ုပ်တို့မရနိုင်ဟု ဆိုလိုသည်။ x အနီးတွင် 2 အဖြစ် f(x) တန်ဖိုးကို တွက်ကြည့်ရအောင်။
| x | f(x) | x | f(x) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.99 | ၃. |
x သည် 2 သို့ ချဉ်းကပ်သောအခါ၊ တန်ဖိုး၏ \(f(x) = \frac{x^2 - 4}{x-2}\) 4 သို့ ချဉ်းကပ်သည်။ ထို့ကြောင့်၊
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Continuity ကို အမျိုးမျိုးသော နည်းလမ်းများဖြင့် သဘောတရားအရ သတ်မှတ်နိုင်သည်။ စာမျက်နှာမှ ဘောပင်ကို မရုတ်သိမ်းဘဲ ၎င်း၏ဂရပ်ကို ဘောပင်ဖြင့် ခြေရာခံနိုင်လျှင် လုပ်ဆောင်ချက်သည် အဆက်မပြတ်ဖြစ်သည်။ ၎င်း၏ဂရပ်သည် အပေါက်များ၊ ကွက်လပ်များ သို့မဟုတ် ကွဲအက်ခြင်းမရှိသော မပြိုကွဲသောမျဉ်းကွေးဖြစ်ပါက လုပ်ဆောင်ချက်သည် စဉ်ဆက်မပြတ်ဖြစ်သည်။ အောက်ဖော်ပြပါ ဂရပ်များသည် စဉ်ဆက်မပြတ် လုပ်ဆောင်ချက်များကို ကိုယ်စားပြုသည်။
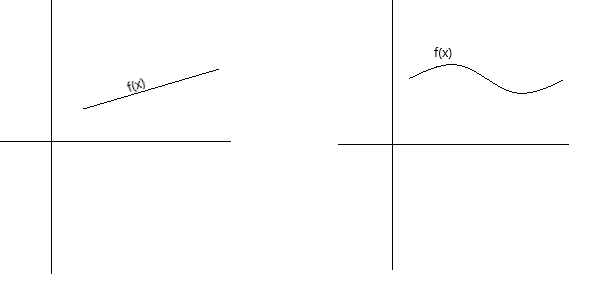
အဆက်ပြတ်ခြင်း၏ ပိုမိုတရားဝင်သော အဓိပ္ပါယ်ဖွင့်ဆိုချက်အနေဖြင့်၊ အောက်ပါအခြေအနေများနှင့် ကိုက်ညီပါက လုပ်ဆောင်ချက် f(x) သည် အမှတ် x = a တွင် ဆက်တိုက်ဖြစ်နေသည်ဟု ဆိုနိုင်ပါသည်။
(i) f(a) ကို သတ်မှတ်ထားသည် (ii) \(\lim\limits_{x \to a} f(x) \) ရှိပါသည် (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
အောက်ဖော်ပြပါ ဂရပ်များတွင် ဖော်ပြထားသော လုပ်ဆောင်ချက်များကို စစ်ဆေးပါ။ လုပ်ဆောင်ချက်နှစ်ခုလုံးသည် ဆက်တိုက်အခြေအနေသုံးရပ်ကို မကျေနပ်နိုင်ပါ။
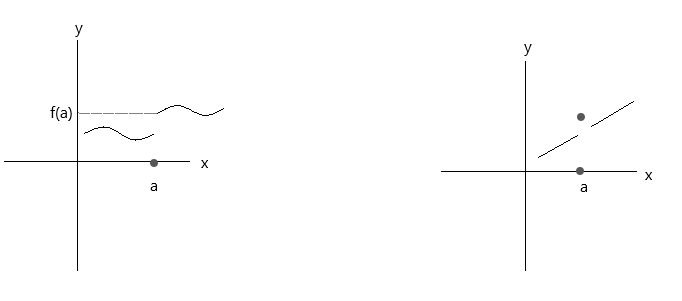
ပထမဂရပ်ကိုကြည့်ပါ၊ \(\lim\limits_{x \to a} f(x) \) = f(a) သည် ညာဘက်ခြမ်းမှ x တန်ဖိုး 'a' သို့ ချဉ်းကပ်ပါက အမှတ်အမှန်ဖြစ်သည်။ သို့သော် x သည် ဘယ်ဘက်မှ တန်ဖိုး 'a' သို့ ချဉ်းကပ်ပါက f(x) သည် f(a) သို့ ချဉ်းကပ်မည်မဟုတ်ပါ၊ ထို့ကြောင့် ၎င်းသည် အဆက်မပြတ်လုပ်ဆောင်မှုတစ်ခုဖြစ်သည်။