क्याल्कुलसका दुवै भागहरू, डिफरेंशियल र इन्टिग्रल क्याल्कुलस सीमाहरूमा आधारित छन्।
सीमा भनेको कुनै बिन्दुको सबैभन्दा राम्रो भविष्यवाणी हो। जब हामी प्रत्यक्ष रूपमा परिणाम गणना गर्न सक्दैनौं तब यसले हामीलाई अनुमान दिन्छ। सीमा भनेको त्यो मान हो जुन प्रकार्यले 'नजिकै पुग्छ' किनकि इनपुटले केही मान 'नजिकै पुग्छ'।
एउटा उदाहरण प्रयोग गरेर यो अवधारणा बुझौं।
मानौं f(x) = 4x − 3। x ले मान 3 को नजिक लैजाँदा f(x) को मानहरू गणना गर्नुहोस्। प्रकार्य f(x) = 4x − 3 को लागि ग्राफ हेर्नुहोस्। x 3 को नजिक भएको बिन्दुहरू जाँच गर्नुहोस्।
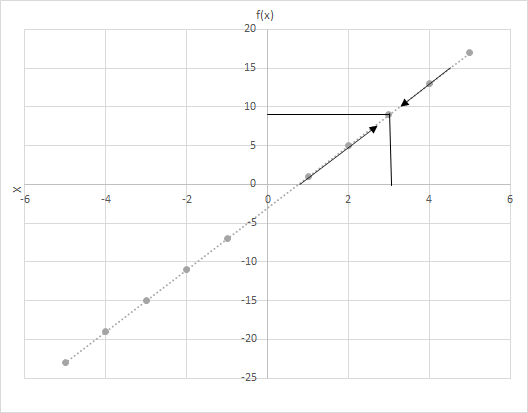
यहाँ दुई परिदृश्यहरू विचार गर्नुहोस्
(i) x बायाँबाट ३ नजिक आउँदैछ र
(ii) x दायाँबाट ३ नजिक आउँदै।
| x | च(x) | x | च(x) | |
| २ | ५ | ४ | १३ | |
| २.२ | ५.८ | ३.५ | ११ | |
| २.५ | ७ | ३.२ | ९.८ | |
| २.८ | ८.२ | ३.१२ | ९.४८ | |
| २.९ | ८.६ | ३.१ | ९.४ | |
| २.९१ | ८.६४ | ३.०९ | ९.३६ | |
| २.९५ | ८.८ | ३.०५ | ९.२ | |
| २.९९९ | ८.९९६ | ३.०१ | ९.०४ |
के तपाईंले अन्तिम पङ्क्ति देख्नुहुन्छ? दुवै अवस्थामा x ३ नजिक पुग्दा, f(x) ९ नजिक पुग्छ। त्यसैले, हामी भन्न सक्छौं:
\(\lim\limits_{x \to 3} f(x) = 9\)
अर्को उदाहरण लिऔं, x २ नजिक पुग्दा f(x) प्रकार्यको सीमा पत्ता लगाउनुहोस्, जहाँ \(f(x) = \frac{x^2 - 4}{x-2}\) , अर्थात् \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
यदि हामीले x को मान २ राख्यौं भने हामीले पाउँछौं: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{अपरिभाषित}\)
यसको अर्थ यो हो कि हामीले अभिव्यक्तिमा x को मान प्रतिस्थापन गरेर सीमाको मान प्राप्त गर्न सक्दैनौं। x २ नजिक पुग्दा f(x) को मान गणना गरौं।
| x | f(x) | x | f(x) |
| १ | ३ | २.५ | ४.५ |
| १.२ | ३.२ | २.२ | ४.२ |
| १.५ | ३.५ | २.१ | ४.१ |
| १.८ | ३.८ | २.०५ | ४.०५ |
| १.९ | ३.९ | २.०१ | ४.०१ |
| १.९९ | ३.९९ |
x २ नजिक पुग्दा, \(f(x) = \frac{x^2 - 4}{x-2}\) को मान ४ नजिक पुग्छ। त्यसैले,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
निरन्तरतालाई केही फरक तरिकाले अवधारणात्मक रूपमा परिभाषित गर्न सकिन्छ। यदि कुनै प्रकार्यको ग्राफ पेनबाट पेन नउठाइकन ट्रेस गर्न सकिन्छ भने त्यो निरन्तर हुन्छ। यदि कुनै प्रकार्यको ग्राफ कुनै प्वाल, खाली ठाउँ वा ब्रेक बिनाको अभंग वक्र हो भने त्यो निरन्तर हुन्छ। तलका ग्राफहरूले निरन्तर प्रकार्यहरूलाई प्रतिनिधित्व गर्छन्।
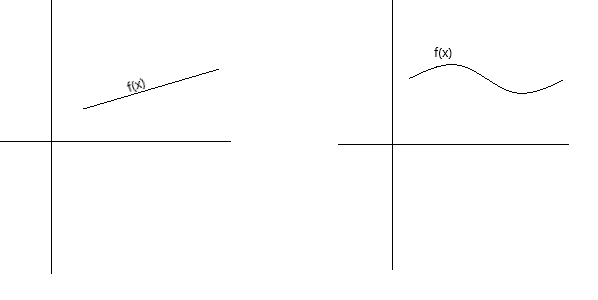
निरन्तरताको औपचारिक परिभाषाको रूपमा, हामी भन्न सक्छौं कि यदि निम्न सर्तहरू पूरा भएमा प्रकार्य f(x) बिन्दु x = a मा निरन्तर हुन्छ:
(i) f(a) परिभाषित गरिएको छ (ii) \(\lim\limits_{x \to a} f(x) \) अवस्थित छ (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
तलका ग्राफहरूमा प्लट गरिएका प्रकार्यहरू जाँच गर्नुहोस्। दुवै प्रकार्यहरूले तीन निरन्तरता सर्तहरू पूरा गर्दैनन्:
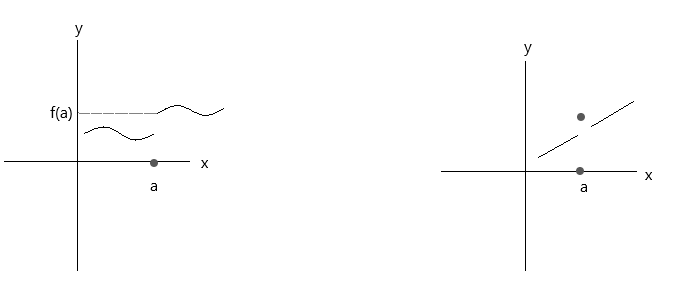
पहिलो ग्राफ हेर्नुहोस्, \(\lim\limits_{x \to a} f(x) \) = f(a) बिन्दु a मा यदि x दायाँ तर्फबाट मान 'a' मा पुग्छ भने सत्य हुन्छ। तर यदि x बायाँ तर्फबाट मान 'a' मा पुग्छ भने, f(x) f(a) मा पुग्दैन, त्यसैले यो एक विच्छेदन प्रकार्य हो।