Beide onderdelen van calculus, differentiaalrekening en integraalrekening, zijn gebaseerd op limieten .
De limiet is de beste voorspelling van een punt. Het geeft ons een schatting wanneer we het resultaat niet direct kunnen berekenen. De limiet is de waarde die de functie 'benadert' wanneer de invoer een bepaalde waarde 'benadert'.
Laten we dit concept aan de hand van een voorbeeld verduidelijken.
Laat f(x) = 4x − 3. Bereken de waarden van f(x) als x de waarde dichter bij 3 brengt. Bekijk de grafiek voor de functie f(x) = 4x − 3. Onderzoek de punten waar x dichter bij 3 ligt.
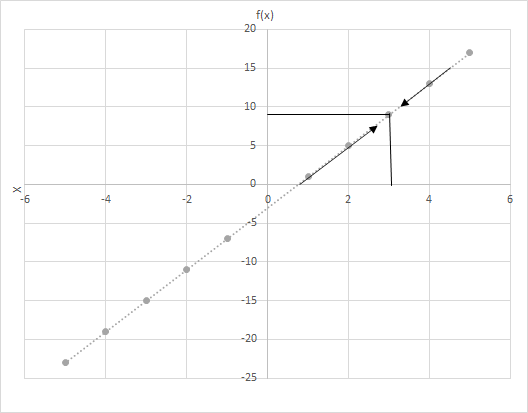
Laten we hier twee scenario's overwegen
(i) x nadert 3 van links en
(ii) x nadert 3 van rechts.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3,5 | 11 | |
| 2,5 | 7 | 3,2 | 9,8 | |
| 2,8 | 8,2 | 3,12 | 9,48 | |
| 2,9 | 8,6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3.01 | 9.04 |
Zie je de laatste rij? In beide gevallen, als x 3 nadert, nadert f(x) 9. Daarom kunnen we zeggen:
\(\lim\limits_{x \to 3} f(x) = 9\)
Laten we nog een voorbeeld nemen: zoek de limiet voor de functie f(x) als x 2 nadert, waarbij \(f(x) = \frac{x^2 - 4}{x-2}\) , d.w.z. \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Als we de waarde van x op 2 zetten krijgen we: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{ongedefinieerd}\)
Dit impliceert dat we de waarde van de limiet niet kunnen krijgen door de waarde van x in de uitdrukking te substitueren. Laten we de waarde van f(x) berekenen naarmate x 2 nadert.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
Naarmate x 2 nadert, nadert de waarde van \(f(x) = \frac{x^2 - 4}{x-2}\) 4. Daarom,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Continuïteit kan conceptueel op verschillende manieren worden gedefinieerd. Een functie is continu als de grafiek ervan met een pen kan worden gevolgd zonder de pen van de pagina te halen. Een functie is continu als de grafiek ervan een ononderbroken curve is zonder gaten, onderbrekingen of onderbrekingen. De onderstaande grafieken geven continue functies weer.
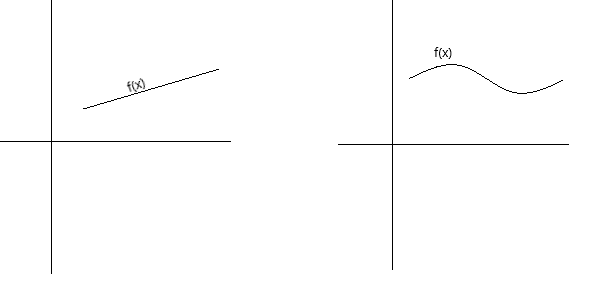
Als een formelere definitie van continuïteit kunnen we zeggen dat een functie f(x) continu is in een punt x = a als aan de volgende voorwaarden wordt voldaan:
(i) f(a) is gedefinieerd (ii) \(\lim\limits_{x \to a} f(x) \) bestaat (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Controleer de functies die in de onderstaande grafieken zijn weergegeven. Beide functies voldoen niet aan de drie continuïteitsvoorwaarden:
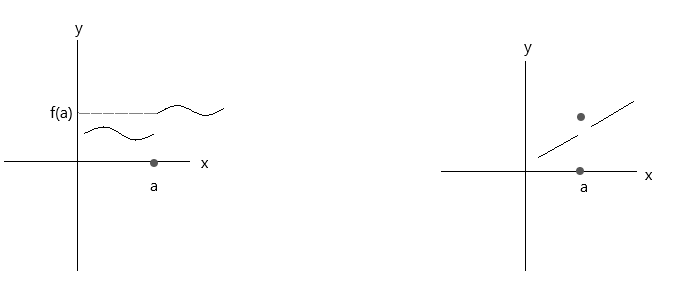
Kijk naar de eerste grafiek, \(\lim\limits_{x \to a} f(x) \) = f(a) in punt a is waar als x waarde 'a' vanaf de rechterkant nadert. Maar als x waarde 'a' vanaf de linkerkant nadert, nadert f(x) f(a) niet, en is het dus een discontinue functie.