Obie części rachunku różniczkowego i całkowego, czyli rachunek różniczkowy i całkowy, opierają się na granicach .
Limit to najlepsza prognoza punktu. Daje nam oszacowanie, gdy nie możemy obliczyć wyniku bezpośrednio. Limit to wartość, do której funkcja „zbliża się”, gdy dane wejściowe „zbliżają się” do pewnej wartości.
Zrozumiemy tę koncepcję na przykładzie.
Niech f(x) = 4x − 3. Oblicz wartości f(x) dla x przyjmującego wartość bliższą 3. Spójrz na wykres funkcji f(x) = 4x − 3. Zbadaj punkty, w których x jest bliższe 3.
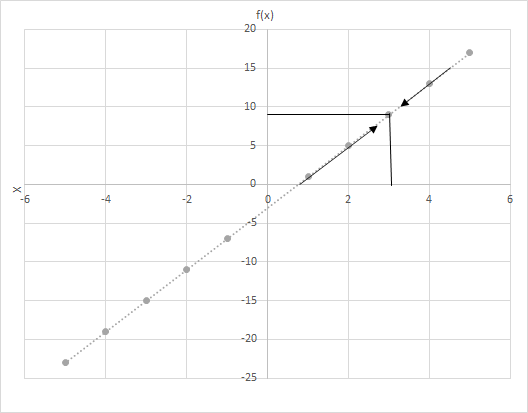
Rozważmy tutaj dwa scenariusze
(i) x zbliżający się do 3 od lewej i
(ii) x zbliża się do 3 od prawej.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2,2 | 5,8 | 3,5 | 11 | |
| 2,5 | 7 | 3,2 | 9,8 | |
| 2,8 | 8,2 | 3,12 | · 9,48 | |
| · 2,9 · | 8,6 | 3,1 | 9,4 | |
| 2,91 | 8,64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3.01 | 9.04 |
Widzisz ostatni wiersz? W obu przypadkach, gdy x zbliża się do 3, f(x) zbliża się do 9. Dlatego możemy powiedzieć:
\(\lim\limits_{x \to 3} f(x) = 9\)
Weźmy inny przykład i znajdźmy granicę funkcji f(x) dla x zbliżającego się do 2, gdzie \(f(x) = \frac{x^2 - 4}{x-2}\) , tj. \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Jeżeli wartość x podstawimy jako 2, otrzymamy: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{niezdefiniowany}\)
Oznacza to, że nie możemy uzyskać wartości granicy, podstawiając wartość x w wyrażeniu. Obliczmy wartość f(x), gdy x zbliża się do 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
Gdy x zbliża się do 2, wartość \(f(x) = \frac{x^2 - 4}{x-2}\) zbliża się do 4. Dlatego
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Ciągłość można zdefiniować koncepcyjnie na kilka różnych sposobów. Funkcja jest ciągła, jeśli jej wykres można narysować długopisem bez odrywania długopisu od strony. Funkcja jest ciągła, jeśli jej wykres jest nieprzerwaną krzywą bez dziur, przerw ani przerw. Poniższe wykresy przedstawiają funkcje ciągłe.
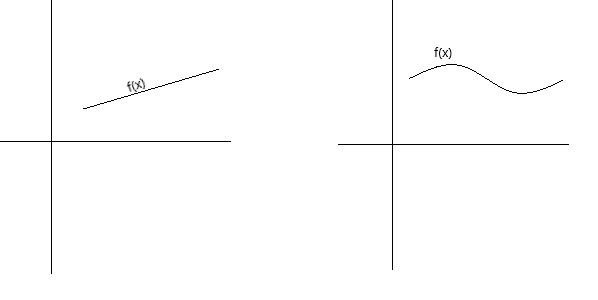
Jako bardziej formalną definicję ciągłości możemy powiedzieć, że funkcja f(x) jest ciągła w punkcie x = a, jeżeli spełnione są następujące warunki:
(i) f(a) jest zdefiniowane (ii) \(\lim\limits_{x \to a} f(x) \) istnieje (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Sprawdź funkcje przedstawione na poniższych wykresach. Obie funkcje nie spełniają trzech warunków ciągłości:
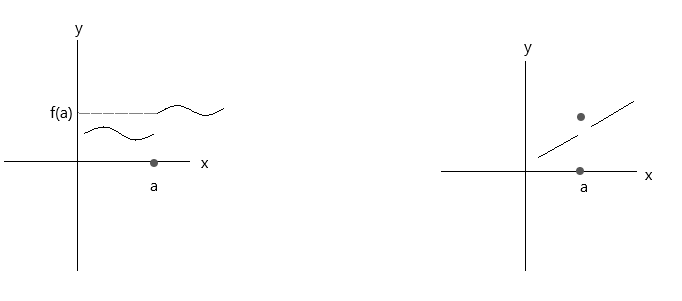
Spójrz na pierwszy wykres, \(\lim\limits_{x \to a} f(x) \) = f(a) w punkcie a jest prawdziwe, jeśli x zbliża się do wartości 'a' od prawej strony. Ale jeśli x zbliża się do wartości 'a' od lewej strony, f(x) nie zbliża się do f(a), zatem jest funkcją nieciągłą.