Ambas as partes do cálculo, cálculo diferencial e integral, são baseadas em limites .
Limite é a melhor previsão de um ponto. Ele nos fornece uma estimativa quando não podemos calcular o resultado diretamente. Limite é o valor do qual a função se aproxima conforme a entrada se aproxima de algum valor.
Vamos entender esse conceito usando um exemplo.
Seja f(x) = 4x − 3. Calcule os valores de f(x) quando x assumir um valor mais próximo de 3. Observe o gráfico da função f(x) = 4x − 3. Examine os pontos onde x está mais próximo de 3.
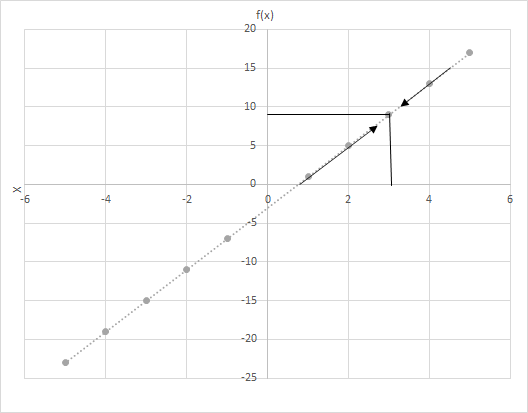
Considere dois cenários aqui
(i) x aproximando-se de 3 da esquerda e
(ii) x aproximando-se de 3 da direita.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2,2 | 5,8 | 3,5 | 11 | |
| 2,5 | 7 | 3,2 | 9,8 | |
| 2,8 | 8,2 | 3,12 | 9,48 | |
| 2,9 | 8,6 | 3,1 | 9,4 | |
| 2,91 | 8,64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3,01 | 9,04 |
Você vê a última linha? Em ambos os casos, quando x se aproxima de 3, f(x) se aproxima de 9. Portanto, podemos dizer:
\(\lim\limits_{x \to 3} f(x) = 9\)
Vamos pegar outro exemplo, encontrar o limite para a função f(x) quando x se aproxima de 2, onde \(f(x) = \frac{x^2 - 4}{x-2}\) , ou seja, \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Se colocarmos o valor de x como 2, obtemos: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{indefinido}\)
Isso implica que não podemos obter o valor do limite substituindo o valor de x na expressão. Vamos calcular o valor de f(x) quando x se aproxima de 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
À medida que x se aproxima de 2, o valor de \(f(x) = \frac{x^2 - 4}{x-2}\) se aproxima de 4. Portanto,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
A continuidade pode ser definida conceitualmente de algumas maneiras diferentes. Uma função é contínua se seu gráfico puder ser traçado com uma caneta sem levantar a caneta da página. Uma função é contínua se seu gráfico for uma curva contínua, sem buracos, lacunas ou quebras. Os gráficos abaixo representam funções contínuas.
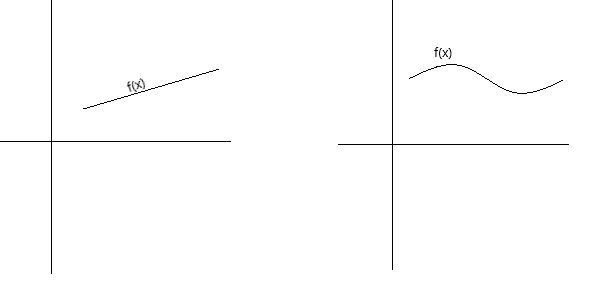
Como definição mais formal de continuidade, podemos dizer que uma função f(x) é contínua em um ponto x = a se as seguintes condições forem atendidas:
(i) f(a) é definido (ii) \(\lim\limits_{x \to a} f(x) \) existe (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Verifique as funções representadas nos gráficos abaixo. Ambas as funções não satisfazem as três condições de continuidade:
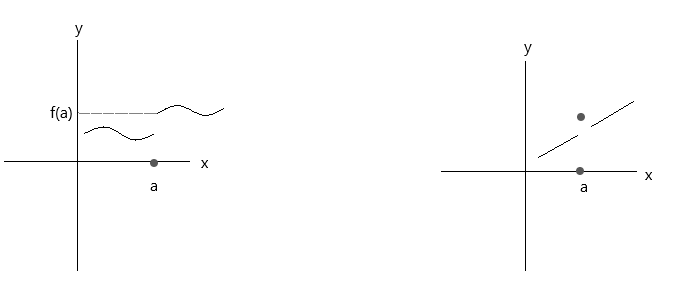
Observe o primeiro gráfico: \(\lim\limits_{x \to a} f(x) \) = f(a) no ponto a é verdadeiro se x se aproxima do valor 'a' pelo lado direito. Mas se x se aproxima do valor 'a' pelo lado esquerdo, f(x) não se aproxima de f(a), portanto, é uma função descontínua.