Обе части исчисления, дифференциальное и интегральное, основаны на пределах .
Предел — это наилучшее предсказание точки. Он дает нам оценку, когда мы не можем вычислить результат напрямую. Предел — это значение, к которому функция «приближается», когда входные данные «приближаются» к некоторому значению.
Давайте разберем эту концепцию на примере.
Пусть f(x) = 4x − 3. Вычислите значения f(x), когда x принимает значение, близкое к 3. Посмотрите на график функции f(x) = 4x − 3. Изучите точки, где x ближе к 3.
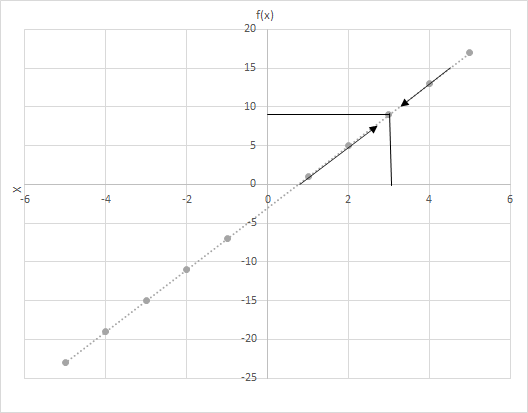
Рассмотрим здесь два сценария.
(i) x приближается к 3 слева и
(ii) x приближается к 3 справа.
| х | ф(х) | х | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2,2 | 5,8 | 3,5 | 11 | |
| 2,5 | 7 | 3,2 | 9,8 | |
| 2,8 | 8,2 | 3,12 | 9,48 | |
| 2,9 | 8,6 | 3,1 | 9,4 | |
| 2,91 | 8,64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3.01 | 9.04 |
Видите последнюю строку? В обоих случаях, когда x стремится к 3, f(x) стремится к 9. Поэтому мы можем сказать:
\(\lim\limits_{x \to 3} f(x) = 9\)
Давайте рассмотрим другой пример: найдем предел для функции f(x), когда x стремится к 2, где \(f(x) = \frac{x^2 - 4}{x-2}\) , т.е. \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Если мы подставим значение x как 2, то получим: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{неопределенный}\)
Это означает, что мы не можем получить значение предела, подставляя значение x в выражение. Давайте вычислим значение f(x), когда x стремится к 2.
| х | f(x) | х | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
Когда x приближается к 2, значение \(f(x) = \frac{x^2 - 4}{x-2}\) приближается к 4. Следовательно,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Непрерывность можно определить концептуально несколькими способами. Функция непрерывна, если ее график можно нарисовать ручкой, не отрывая ее от страницы. Функция непрерывна, если ее график представляет собой непрерывную кривую без отверстий, зазоров или разрывов. Приведенные ниже графики представляют непрерывные функции.
В качестве более формального определения непрерывности можно сказать, что функция f(x) непрерывна в точке x = a, если выполняются следующие условия:
(i) f(a) определено (ii) \(\lim\limits_{x \to a} f(x) \) существует (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Проверьте функции, изображенные на графиках ниже. Обе функции не удовлетворяют трем условиям непрерывности:
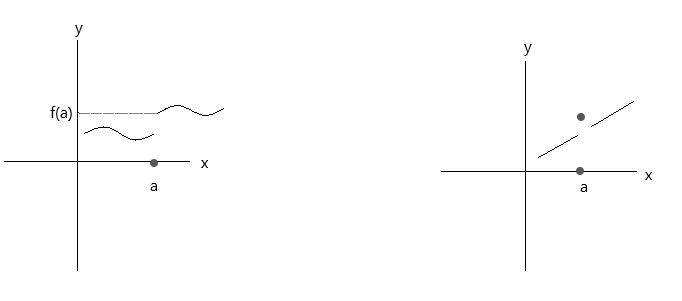
Посмотрите на первый график, \(\lim\limits_{x \to a} f(x) \) = f(a) в точке a истинно, если x приближается к значению 'a' с правой стороны. Но если x приближается к значению 'a' с левой стороны, f(x) не приближается к f(a), следовательно, это разрывная функция.