Të dyja pjesët e analizës matematike, ajo diferenciale dhe ajo integrale, bazohen në kufij .
Limiti është parashikimi më i mirë i një pike. Ai na jep një vlerësim kur nuk mund ta llogarisim rezultatin drejtpërdrejt. Limiti është vlera së cilës funksioni 'i afrohet' ndërsa hyrja 'i afrohet' një vlere.
Le ta kuptojmë këtë koncept duke përdorur një shembull.
Le të jetë f(x) = 4x − 3. Llogaritni vlerat e f(x) ndërsa x e afron vlerën më shumë me 3. Shikoni grafikun për funksionin f(x) = 4x − 3. Shqyrtoni pikat ku x është më afër 3.
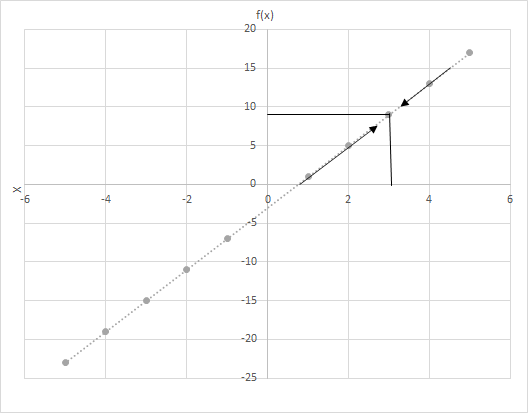
Konsideroni dy skenarë këtu
(i) x i afrohet 3 nga e majta dhe
(ii) x po i afrohet 3 nga e djathta.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3.5 | 11 | |
| 2.5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3.12 | 9.48 | |
| 2.9 | 8.6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3.09 | 9.36 | |
| 2.95 | 8.8 | 3.05 | 9.2 | |
| 2.999 | 8.996 | 3.01 | 9.04 |
A e shihni rreshtin e fundit? Në të dyja rastet, ndërsa x i afrohet 3, f(x) i afrohet 9. Prandaj, mund të themi:
\(\lim\limits_{x \to 3} f(x) = 9\)
Le të marrim një shembull tjetër, të gjejmë limitin për funksionin f(x) ndërsa x i afrohet vlerës 2, ku \(f(x) = \frac{x^2 - 4}{x-2}\) , dmth \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Nëse e vendosim vlerën e x si 2, marrim: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{i papërcaktuar}\)
Kjo nënkupton që nuk mund ta marrim vlerën e limit duke zëvendësuar vlerën e x në shprehje. Le të llogarisim vlerën e f(x) ndërsa x i afrohet vlerës 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.99 | 3.99 |
Ndërsa x i afrohet vlerës 2, vlera e \(f(x) = \frac{x^2 - 4}{x-2}\) i afrohet vlerës 4. Prandaj,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Vazhdimësia mund të përkufizohet konceptualisht në disa mënyra të ndryshme. Një funksion është i vazhdueshëm nëse grafiku i tij mund të vizatohet me stilolaps pa e hequr stilolapsin nga faqja. Një funksion është i vazhdueshëm nëse grafiku i tij është një kurbë e pandërprerë pa vrima, boshllëqe ose ndërprerje. Grafikët më poshtë përfaqësojnë funksione të vazhdueshme.
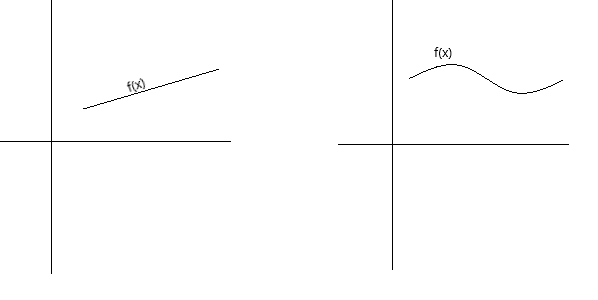
Si një përkufizim më formal i vazhdimësisë, mund të themi se një funksion f(x) është i vazhdueshëm në një pikë x = a nëse plotësohen kushtet e mëposhtme:
(i) f(a) është përcaktuar (ii) \(\lim\limits_{x \to a} f(x) \) ekziston (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Kontrolloni funksionet e paraqitura në grafikët më poshtë. Të dy funksionet nuk i plotësojnë tre kushtet e vazhdimësisë:
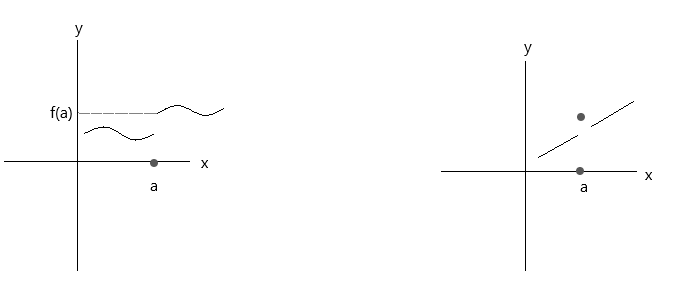
Shikoni grafikun e parë, \(\lim\limits_{x \to a} f(x) \) = f(a) në pikën a është e vërtetë nëse x i afrohet vlerës 'a' nga ana e djathtë. Por nëse x i afrohet vlerës 'a' nga ana e majtë, f(x) nuk po i afrohet f(a), prandaj është një funksion jo i vazhdueshëm.