Båda delarna av kalkylen, differentialkalkyl och integralkalkyl, är baserade på gränsvärden .
Gränsvärdet är den bästa förutsägelsen av en punkt. Det ger oss en uppskattning när vi inte kan beräkna resultatet direkt. Gränsvärdet är det värde som funktionen "närmar sig" när indata "närmar sig" ett visst värde.
Låt oss förstå detta koncept med hjälp av ett exempel.
Låt f(x) = 4x − 3. Beräkna värdena på f(x) när x antar ett värde närmare 3. Titta på grafen för funktionen f(x) = 4x − 3. Undersök punkter där x är närmare 3.
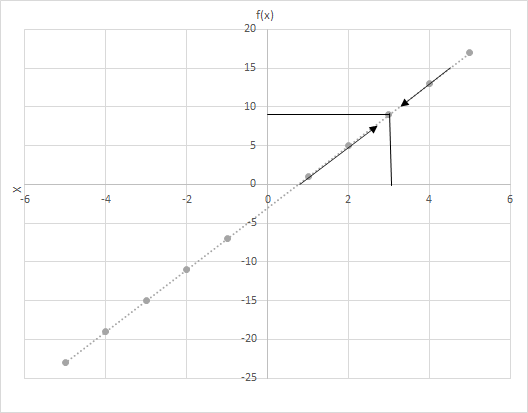
Tänk på två scenarier här
(i) x närmar sig 3 från vänster och
(ii) x närmar sig 3 från höger.
| x | f(x) | x | f(x) | |
| ² | 5 | 4 | 13 | |
| 2,2 | 5,8 | 3,5 | 11 | |
| 2,5 | 7 | 3,2 | 9,8 | |
| 2,8 | 8,2 | 3,12 | 9,48 | |
| 2,9 | 8,6 | 3,1 | 9,4 | |
| 2,91 | 8,64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3,01 | 9,04 |
Ser du den sista raden? I båda fallen, när x närmar sig 3, närmar sig f(x) 9. Därför kan vi säga:
\(\lim\limits_{x \to 3} f(x) = 9\)
Låt oss ta ett annat exempel, hitta gränsvärdet för funktionen f(x) när x närmar sig 2, där \(f(x) = \frac{x^2 - 4}{x-2}\) , dvs. \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Om vi sätter värdet på x som 2 får vi: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{odefinierad}\)
Detta innebär att vi inte kan få värdet på gränsvärdet genom att sätta in värdet på x i uttrycket. Låt oss beräkna värdet på f(x) när x närmar sig 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
När x närmar sig 2, närmar sig värdet av \(f(x) = \frac{x^2 - 4}{x-2}\) 4. Därför,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Kontinuitet kan definieras konceptuellt på några olika sätt. En funktion är kontinuerlig om dess graf kan ritas med en penna utan att lyfta pennan från sidan. En funktion är kontinuerlig om dess graf är en obruten kurva utan hål, mellanrum eller brott. Graferna nedan representerar kontinuerliga funktioner.
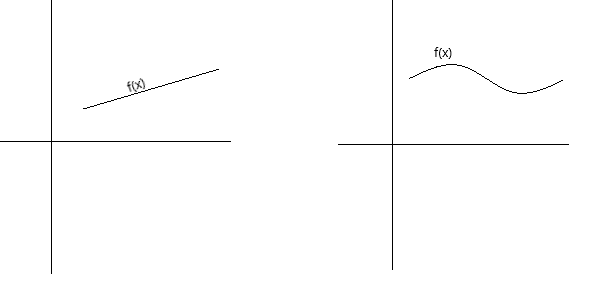
Som en mer formell definition av kontinuitet kan vi säga att en funktion f(x) är kontinuerlig i punkten x = a om följande villkor är uppfyllda:
(i) f(a) är definierad (ii) \(\lim\limits_{x \to a} f(x) \) existerar (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Kontrollera funktionerna som är ritade i graferna nedan. Inga av funktionerna uppfyller de tre kontinuitetsvillkoren:
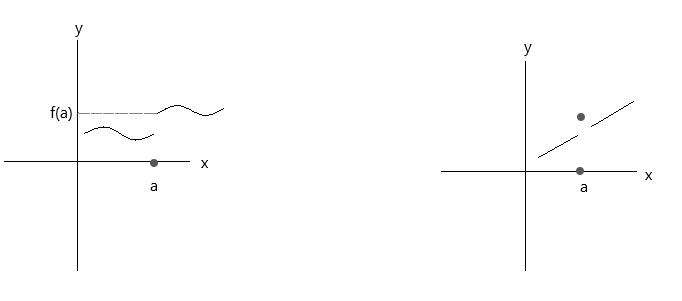
Titta på den första grafen, \(\lim\limits_{x \to a} f(x) \) = f(a) i punkt a är sant om x närmar sig värdet 'a' från höger sida. Men om x närmar sig värdet 'a' från vänster sida, närmar sig f(x) inte f(a), alltså en diskontinuerlig funktion.