Sehemu zote mbili za calculus, Differential na Integral calculus zinatokana na Mipaka .
Kikomo ni utabiri bora wa uhakika. Inatupa makadirio wakati hatuwezi kukokotoa matokeo moja kwa moja. Kikomo ni thamani ambayo chaguo za kukokotoa 'hukaribia' kama ingizo 'inapokaribia' thamani fulani.
Hebu tuelewe dhana hii kwa kutumia mfano.
Acha f(x) = 4x − 3. Kokotoa thamani za f(x) kama x inavyochukua thamani karibu na 3. Angalia grafu ya chaguo za kukokotoa f(x) = 4x - 3. Chunguza pointi ambapo x iko karibu na 3.
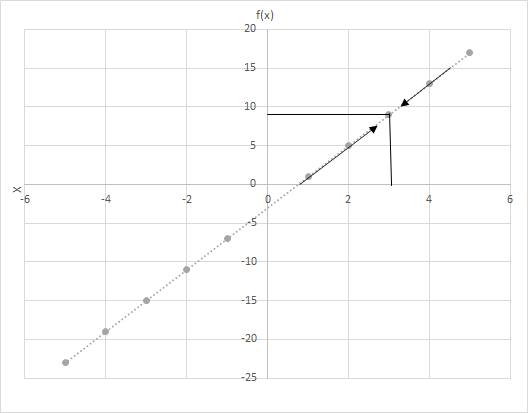
Fikiria hali mbili hapa
(i) x inakaribia 3 kutoka kushoto na
(ii) x inakaribia 3 kutoka kulia.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3.5 | 11 | |
| 2.5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3.12 | 9.48 | |
| 2.9 | 8.6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3.09 | 9.36 | |
| 2.95 | 8.8 | 3.05 | 9.2 | |
| 2.999 | 8.996 | 3.01 | 9.04 |
Je, unaona safu mlalo ya mwisho? Katika visa vyote viwili x inakaribia 3, f(x) inakaribia 9. Kwa hivyo, tunaweza kusema:
\(\lim\limits_{x \to 3} f(x) = 9\)
Hebu tuchukue mfano mwingine, tutafute kikomo cha chaguo za kukokotoa f(x) x inapokaribia 2, ambapo \(f(x) = \frac{x^2 - 4}{x-2}\) , yaani \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Tukiweka thamani ya x kama 2 tunapata: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{isiyofafanuliwa}\)
Hii ina maana kwamba hatuwezi kupata thamani ya kikomo kwa kubadilisha thamani ya x katika usemi. Wacha tuhesabu thamani ya f(x) kadri x inavyokaribia 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.99 | 3. |
x inapokaribia 2, thamani ya \(f(x) = \frac{x^2 - 4}{x-2}\) inakaribia 4. Kwa hivyo,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
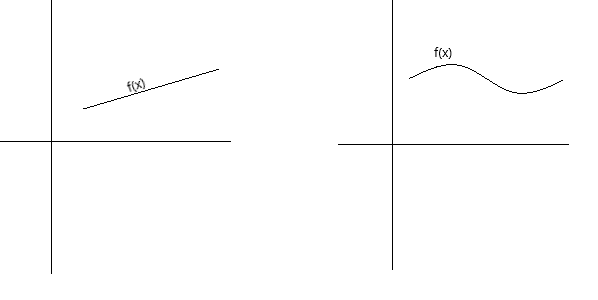
Mwendelezo unaweza kufafanuliwa kimawazo kwa njia chache tofauti. Kitendaji kinaendelea, ikiwa grafu yake inaweza kufuatiliwa kwa kalamu bila kuinua kalamu kutoka kwa ukurasa. Chaguo za kukokotoa ni endelevu ikiwa grafu yake ni mkunjo usiokatika bila mashimo, mapengo au migawanyiko. Grafu zilizo hapa chini zinawakilisha utendakazi endelevu.
Kama ufafanuzi rasmi zaidi wa mwendelezo, tunaweza kusema chaguo la kukokotoa f(x) linaendelea kwa uhakika x = a ikiwa masharti yafuatayo yametimizwa:
(i) f(a) imefafanuliwa (ii) \(\lim\limits_{x \to a} f(x) \) ipo (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Angalia vitendaji vilivyopangwa katika grafu hapa chini. Kazi zote mbili hazikidhi masharti matatu ya mwendelezo:
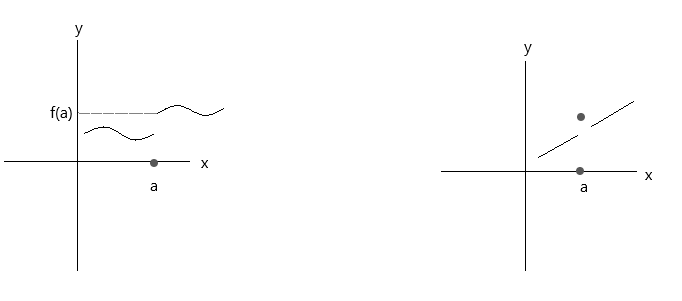
Angalia grafu ya kwanza, \(\lim\limits_{x \to a} f(x) \) = f(a) kwa uhakika a ni kweli ikiwa x inakaribia thamani 'a' kutoka upande wa kulia. Lakini ikiwa x inakaribia thamani 'a' kutoka upande wa kushoto, f(x) haikaribii f(a), kwa hivyo ni kazi isiyoendelea.