แคลคูลัสทั้ง 2 ส่วน คือ แคลคูลัสเชิงอนุพันธ์และแคลคูลัสเชิงปริพันธ์ ล้วนมีพื้นฐานอยู่บน ลิมิต
ลิมิตคือการทำนายจุดที่ดีที่สุด ซึ่งจะให้การประมาณค่าเมื่อเราไม่สามารถคำนวณผลลัพธ์ได้โดยตรง ลิมิตคือค่าที่ฟังก์ชัน 'เข้าใกล้' เมื่ออินพุต 'เข้าใกล้' ค่าบางค่า
มาทำความเข้าใจแนวคิดนี้โดยใช้ตัวอย่างกัน
ให้ f(x) = 4x − 3 คำนวณค่าของ f(x) เมื่อ x มีค่าใกล้เคียงกับ 3 มากขึ้น ดูที่กราฟของฟังก์ชัน f(x) = 4x − 3 ตรวจสอบจุดที่ x ใกล้เคียงกับ 3 มากขึ้น
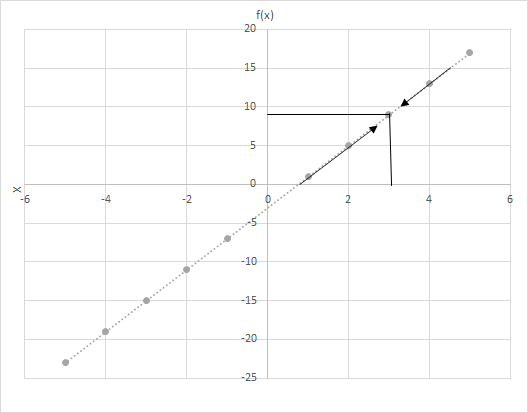
พิจารณาสองสถานการณ์ที่นี่
(i) x เข้าใกล้ 3 จากซ้ายและ
(ii) x เข้าใกล้ 3 จากทางขวา
| x | ฟ(x) | x | ฟ(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3.5 | 11 | |
| 2.5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3.12 | 9.48 | |
| 2.9 | 8.6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3.09 | 9.36 | |
| 2.95 | 8.8 | 3.05 | 9.2 | |
| 2.999 | 8.996 | 3.01 | 9.04 |
คุณเห็นแถวสุดท้ายไหม ในทั้งสองกรณี เมื่อ x เข้าใกล้ 3, f(x) จะเข้าใกล้ 9 ดังนั้น เราสามารถพูดได้ว่า:
\(\lim\limits_{x \to 3} f(x) = 9\)
มาดูตัวอย่างอื่นกัน หาลิมิตของฟังก์ชัน f(x) เมื่อ x เข้าใกล้ 2 โดยที่ \(f(x) = \frac{x^2 - 4}{x-2}\) หรือ \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
ถ้าเราใส่ค่า x เป็น 2 เราจะได้: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{ไม่ระบุ}\)
นั่นหมายความว่าเราไม่สามารถหาค่าลิมิตได้โดยการแทนค่า x ในนิพจน์ ลองคำนวณค่าของ f(x) เมื่อ x เข้าใกล้ 2
| x | ฟ(x) | x | ฟ(x) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.99 | 3.99 |
เมื่อ x เข้าใกล้ 2 ค่าของ \(f(x) = \frac{x^2 - 4}{x-2}\) จะเข้าใกล้ 4 ดังนั้น
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
ความต่อเนื่อง สามารถกำหนดได้ทางแนวคิดในหลายวิธี ฟังก์ชันจะต่อเนื่องหากกราฟของฟังก์ชันสามารถวาดตามได้ด้วยปากกาโดยไม่ต้องยกปากกาออกจากหน้ากระดาษ ฟังก์ชันจะต่อเนื่องหากกราฟของฟังก์ชันเป็นเส้นโค้งที่ไม่ขาดตอน ไม่มีรู ช่องว่าง หรือจุดแตกหัก กราฟด้านล่างแสดงฟังก์ชันต่อเนื่อง
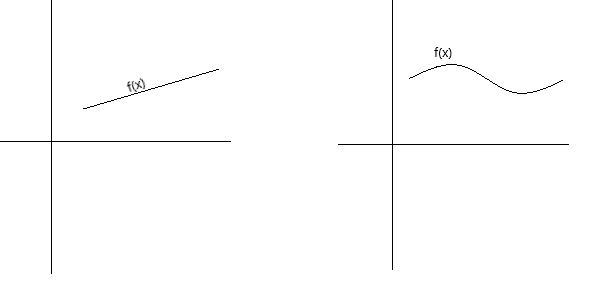
จากคำจำกัดความที่เป็นทางการมากขึ้นของความต่อเนื่อง เราสามารถกล่าวได้ว่าฟังก์ชัน f(x) ต่อเนื่องที่จุด x = a หากเป็นไปตามเงื่อนไขต่อไปนี้:
(i) f(a) ถูกกำหนด (ii) \(\lim\limits_{x \to a} f(x) \) มีอยู่ (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
ตรวจสอบฟังก์ชันที่แสดงในกราฟด้านล่าง ฟังก์ชันทั้งสองไม่เป็นไปตามเงื่อนไขความต่อเนื่องทั้งสามประการ:
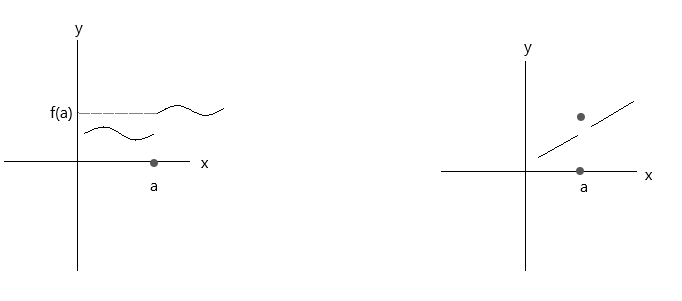
ดูที่กราฟแรก \(\lim\limits_{x \to a} f(x) \) = f(a) ที่จุด a เป็นจริงถ้า x เข้าใกล้ค่า 'a' จากด้านขวา แต่ถ้า x เข้าใกล้ค่า 'a' จากด้านซ้าย f(x) จะไม่เข้าใกล้ f(a) ดังนั้นจึงเป็นฟังก์ชันไม่ต่อเนื่อง