Ang parehong bahagi ng calculus, Differential at Integral calculus ay batay sa Limits .
Ang limitasyon ay ang pinakamahusay na hula ng isang punto. Nagbibigay ito sa amin ng pagtatantya kapag hindi namin direktang makalkula ang resulta. Ang limitasyon ay ang value na 'lumalapit' ng function habang 'lumalapit' ang input sa ilang value.
Unawain natin ang konseptong ito gamit ang isang halimbawa.
Hayaan ang f(x) = 4x − 3. Kuwentahin ang mga halaga ng f(x) habang ang x ay mas malapit sa 3. Tingnan ang graph para sa function na f(x) = 4x − 3. Suriin ang mga punto kung saan ang x ay mas malapit sa 3.
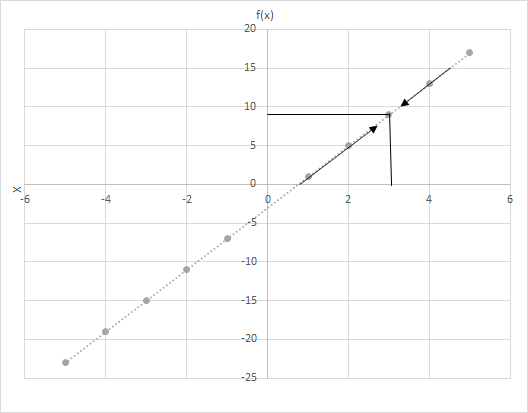
Isaalang-alang ang dalawang senaryo dito
(i) x na lumalapit sa 3 mula sa kaliwa at
(ii) x na lumalapit sa 3 mula sa kanan.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3.5 | 11 | |
| 2.5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3.12 | 9.48 | |
| 2.9 | 8.6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3.09 | 9.36 | |
| 2.95 | 8.8 | 3.05 | 9.2 | |
| 2.999 | 8.996 | 3.01 | 9.04 |
Nakikita mo ba ang huling hilera? Sa parehong mga kaso habang ang x ay lumalapit sa 3, ang f(x) ay lumalapit sa 9. Samakatuwid, maaari nating sabihin:
\(\lim\limits_{x \to 3} f(x) = 9\)
Kumuha tayo ng isa pang halimbawa, hanapin ang limitasyon para sa function na f(x) habang papalapit ang x sa 2, kung saan \(f(x) = \frac{x^2 - 4}{x-2}\) , ibig sabihin, \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Kung ilalagay natin ang halaga ng x bilang 2 makukuha natin: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{hindi natukoy}\)
Ito ay nagpapahiwatig na hindi natin makukuha ang halaga ng limitasyon sa pamamagitan ng pagpapalit ng halaga ng x sa expression. Kalkulahin natin ang halaga ng f(x) habang papalapit ang x sa 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.99 | 3.01 |
Habang lumalapit ang x sa 2, ang halaga ng \(f(x) = \frac{x^2 - 4}{x-2}\) ay lumalapit sa 4. Samakatuwid,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Ang pagpapatuloy ay maaaring tukuyin sa konsepto sa ilang magkakaibang paraan. Ang isang function ay tuluy-tuloy, kung ang graph nito ay maaaring masubaybayan gamit ang isang panulat nang hindi inaalis ang panulat mula sa pahina. Ang isang function ay tuluy-tuloy kung ang graph nito ay isang walang putol na curve na walang mga butas, gaps, o break. Ang mga graph sa ibaba ay kumakatawan sa mga tuluy-tuloy na function.
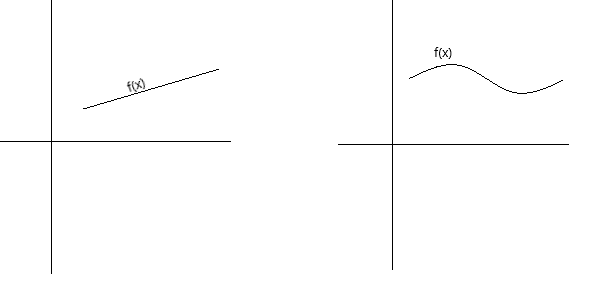
Bilang mas pormal na kahulugan ng pagpapatuloy, masasabi nating ang isang function na f(x) ay tuloy-tuloy sa isang punto x = a kung ang mga sumusunod na kundisyon ay natutugunan:
(i) f(a) ay tinukoy (ii) \(\lim\limits_{x \to a} f(x) \) ay umiiral (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Suriin ang mga function na naka-plot sa mga graph sa ibaba. Ang parehong mga pag-andar ay hindi nakakatugon sa tatlong kondisyon ng pagpapatuloy:
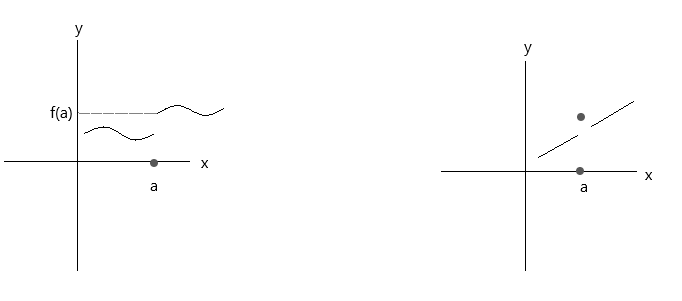
Tingnan ang unang graph, \(\lim\limits_{x \to a} f(x) \) = f(a) sa punto a ay totoo kung ang x ay lumalapit sa value na 'a' mula sa kanang bahagi. Ngunit kung ang x ay lumalapit sa halagang 'a' mula sa kaliwang bahagi, ang f(x) ay hindi lumalapit sa f(a), kaya ito ay isang discontinuous function.