Kalkülüsün her iki bölümü, hem Diferansiyel hem de İntegral hesap, Limitlere dayanır.
Limit, bir noktanın en iyi tahminidir. Sonucu doğrudan hesaplayamadığımızda bize bir tahmin verir. Limit, girdi bir değere 'yaklaştıkça' fonksiyonun 'yaklaştığı' değerdir.
Bu kavramı bir örnekle anlamaya çalışalım.
f(x) = 4x − 3 olsun. f(x) değerlerini, x 3'e yaklaştıkça hesaplayın. f(x) = 4x − 3 fonksiyonunun grafiğine bakın. x'in 3'e yakın olduğu noktaları inceleyin.
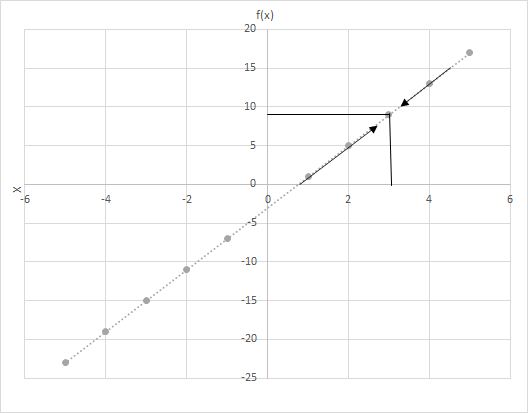
Burada iki senaryoyu ele alalım
(i) x soldan 3'e yaklaşıyor ve
(ii) x sağdan 3'e yaklaşıyor.
| x | f(x) | xf | (x) | |
| 2 | 5 | 4 | 13 | |
| 2,2 | 5,8 | 3,5 | 11 | |
| 2,5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3.12 | 9.48 | |
| 2.9 | 8.6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3.09 | 9.36 | |
| 2.95 | 8.8 | 3.05 | 9.2 | |
| 2.999 | 8.996 | 3.01 | 9.04 |
Son satırı görüyor musunuz? Her iki durumda da x 3'e yaklaşırken, f(x) 9'a yaklaşır. Bu nedenle şunu söyleyebiliriz:
\(\lim\limits_{x \to 3} f(x) = 9\)
Başka bir örnek alalım, x 2'ye yaklaşırken f(x) fonksiyonunun limitini bulalım, burada \(f(x) = \frac{x^2 - 4}{x-2}\) , yani \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
x değerini 2 olarak koyarsak şunu elde ederiz: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{tanımlanmamış}\)
Bu, x değerini ifadeye koyarak limit değerini elde edemeyeceğimiz anlamına gelir. x 2'ye yaklaşırken f(x) değerini hesaplayalım.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
x 2'ye yaklaştıkça, \(f(x) = \frac{x^2 - 4}{x-2}\) değeri 4'e yaklaşır. Bu nedenle,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Süreklilik kavramsal olarak birkaç farklı şekilde tanımlanabilir. Bir fonksiyon, grafiği kalem sayfadan kaldırılmadan bir kalemle izlenebiliyorsa süreklidir. Bir fonksiyon, grafiği delik, boşluk veya kırılma içermeyen kesintisiz bir eğriyse süreklidir. Aşağıdaki grafikler sürekli fonksiyonları temsil eder.
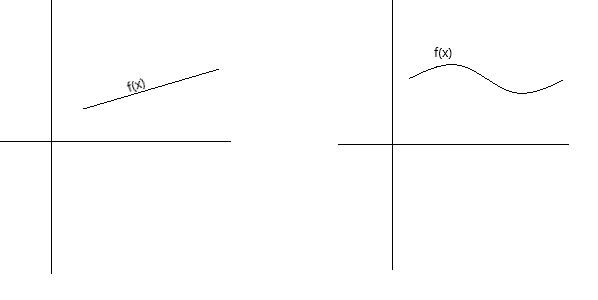
Sürekliliğin daha resmi bir tanımı olarak, aşağıdaki koşullar sağlanıyorsa bir f(x) fonksiyonunun x = a noktasında sürekli olduğunu söyleyebiliriz:
(i) f(a) tanımlanmıştır (ii) \(\lim\limits_{x \to a} f(x) \) vardır (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Aşağıdaki grafiklerde çizilen fonksiyonları kontrol edin. Her iki fonksiyon da üç süreklilik koşulunu karşılamıyor:
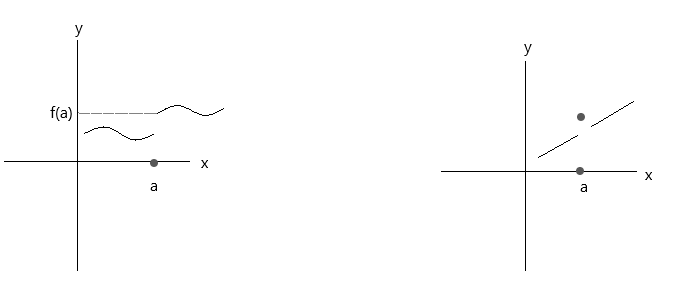
İlk grafiğe bakalım, \(\lim\limits_{x \to a} f(x) \) = f(a) a noktasında, x 'a' değerine sağ taraftan yaklaşıyorsa doğrudur. Ancak x 'a' değerine sol taraftan yaklaşıyorsa, f(x) f(a)'ya yaklaşmamaktadır, dolayısıyla süreksiz bir fonksiyondur.