Обидві частини математичного аналізу, диференціальне та інтегральне числення, базуються на границях .
Границя — це найкраще передбачення точки. Вона дає нам оцінку, коли ми не можемо обчислити результат безпосередньо. Границя — це значення, до якого «наближається» функція, коли вхідні дані «наближаються» до деякого значення.
Давайте розберемося з цією концепцією на прикладі.
Нехай f(x) = 4x − 3. Обчисліть значення f(x), коли x набуває значення ближче до 3. Подивіться на графік функції f(x) = 4x − 3. Розгляньте точки, де x ближче до 3.
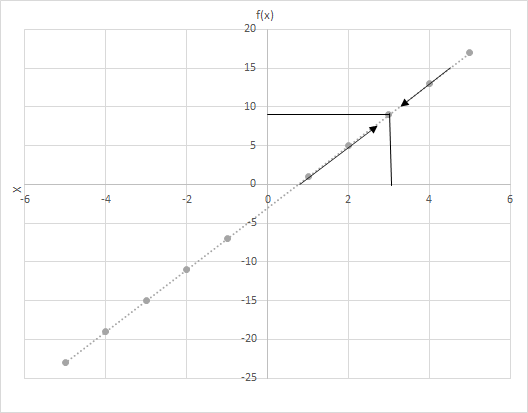
Розглянемо тут два сценарії
(i) x наближається до 3 зліва та
(ii) x наближається до 3 справа.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3,5 | 11 | |
| 2,5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3,12 | 9,48 | |
| 2,9 | 8,6 | 3,1 | 9,4 | |
| 2,91 | 8,64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3.01 | 9.04 |
Бачите останній рядок? В обох випадках, коли x прямує до 3, f(x) прямує до 9. Отже, можна сказати:
\(\lim\limits_{x \to 3} f(x) = 9\)
Візьмемо інший приклад, знайдемо границю функції f(x) при наближенні x до 2, де \(f(x) = \frac{x^2 - 4}{x-2}\) , тобто \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Якщо ми поставимо значення x як 2, то отримаємо: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{невизначено}\)
Це означає, що ми не можемо отримати значення граничної функції, підставляючи значення x у вираз. Давайте обчислимо значення f(x), коли x прямує до 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
Коли x наближається до 2, значення \(f(x) = \frac{x^2 - 4}{x-2}\) наближається до 4. Отже,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Неперервність можна концептуально визначити кількома різними способами. Функція є неперервною, якщо її графік можна простежити ручкою, не відриваючи її від сторінки. Функція є неперервною, якщо її графік є нерозривною кривою без дірок, прогалин або розривів. Графіки нижче представляють неперервні функції.
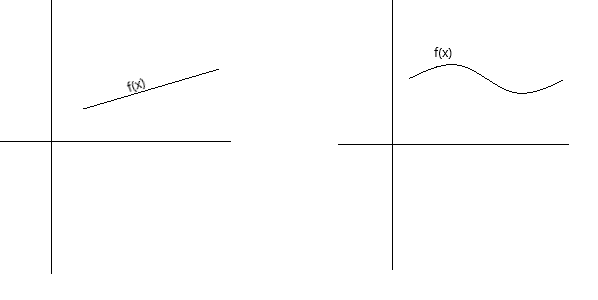
Як більш формальне визначення неперервності, можна сказати, що функція f(x) є неперервною в точці x = a, якщо виконуються такі умови:
(i) f(a) визначено (ii) \(\lim\limits_{x \to a} f(x) \) існує (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Перевірте функції, зображені на графіках нижче. Обидві функції не задовольняють три умови неперервності:
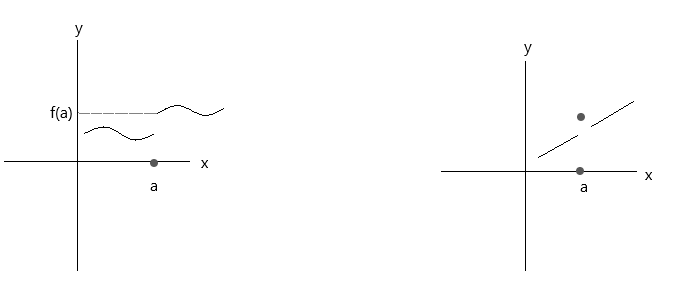
Подивіться на перший графік, \(\lim\limits_{x \to a} f(x) \) = f(a) у точці a є істинним, якщо x наближається до значення 'a' справа. Але якщо x наближається до значення 'a' зліва, f(x) не наближається до f(a), отже, це розривна функція.