کیلکولس کے دونوں حصے، تفریق اور انٹیگرل کیلکولس حدود پر مبنی ہیں۔
حد ایک نقطہ کی بہترین پیشین گوئی ہے۔ یہ ہمیں ایک تخمینہ دیتا ہے جب ہم براہ راست نتیجہ کی گنتی نہیں کر سکتے ہیں۔ حد وہ قدر ہے جس پر فنکشن 'اپروچ' کرتا ہے جیسا کہ ان پٹ 'تقریر' کچھ قدر کرتا ہے۔
آئیے ایک مثال کے ذریعے اس تصور کو سمجھتے ہیں۔
چلیں f(x) = 4x − 3۔ f(x) کی قدروں کی گنتی کریں کیونکہ x قدر کو 3 کے قریب لے جاتا ہے۔ فنکشن f(x) = 4x − 3 کے لیے گراف کو دیکھیں۔ پوائنٹس کی جانچ کریں جہاں x 3 کے قریب ہے۔
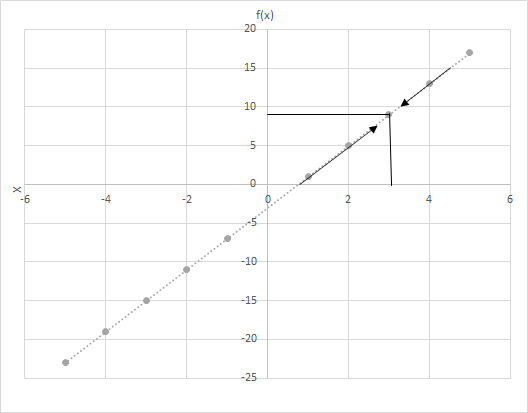
یہاں دو منظرناموں پر غور کریں۔
(i) x بائیں سے 3 کے قریب آرہا ہے اور
(ii) x دائیں سے 3 کے قریب پہنچ رہا ہے۔
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3.5 | 11 | |
| 2.5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3.12 | 9.48 | |
| 2.9 | 8.6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3.09 | 9.36 | |
| 2.95 | 8.8 | 3.05 | 9.2 | |
| 2.999 | 8.996 | 3.01 | 9.04 |
کیا آپ آخری قطار دیکھتے ہیں؟ دونوں صورتوں میں جیسے ہی x 3 کے قریب پہنچتا ہے، f(x) 9 تک پہنچتا ہے۔ لہذا، ہم کہہ سکتے ہیں:
\(\lim\limits_{x \to 3} f(x) = 9\)
آئیے ایک اور مثال لیتے ہیں، فنکشن f(x) کی حد تلاش کریں جیسے ہی x 2 تک پہنچتا ہے، جہاں \(f(x) = \frac{x^2 - 4}{x-2}\) ، یعنی \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
اگر ہم x کی قدر کو 2 کے طور پر رکھتے ہیں تو ہمیں ملتا ہے: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{غیر متعینہ}\)
اس کا مطلب ہے کہ ہم ایکسپریشن میں x کی قدر کو بدل کر حد کی قدر حاصل نہیں کر سکتے۔ آئیے f(x) کی قدر کا حساب لگاتے ہیں جیسے ہی x 2 کے قریب آتا ہے۔
| x | f(x) | x | f(x) |
| 1 | 3 | 2.5 | 4.5 |
| 1.2 | 3.2 | 2.2 | 4.2 |
| 1.5 | 3.5 | 2.1 | 4.1 |
| 1.8 | 3.8 | 2.05 | 4.05 |
| 1.9 | 3.9 | 2.01 | 4.01 |
| 1.993 | ۔ |
جیسے ہی x 2 کے قریب آتا ہے، \(f(x) = \frac{x^2 - 4}{x-2}\) کی قدر 4 تک پہنچ جاتی ہے۔ لہذا،
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
تسلسل کو تصوراتی طور پر چند مختلف طریقوں سے بیان کیا جا سکتا ہے۔ ایک فنکشن مسلسل ہوتا ہے، اگر اس کا گراف صفحہ سے قلم اٹھائے بغیر قلم سے ٹریس کیا جا سکتا ہے۔ ایک فنکشن مسلسل ہے اگر اس کا گراف ایک غیر ٹوٹا ہوا منحنی خطوط ہے جس میں کوئی سوراخ، خلا یا وقفہ نہیں ہے۔ نیچے گراف مسلسل افعال کی نمائندگی کرتے ہیں۔
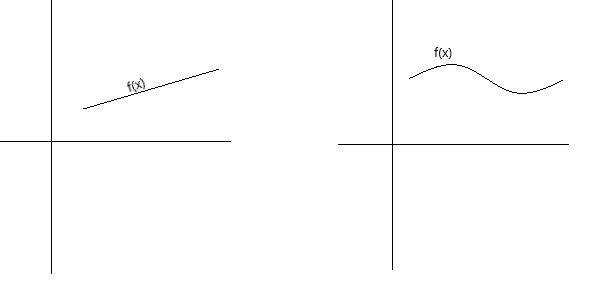
تسلسل کی مزید رسمی تعریف کے طور پر، ہم کہہ سکتے ہیں کہ ایک فنکشن f(x) ایک نقطہ x = a پر مسلسل ہے اگر درج ذیل شرائط پوری ہوں:
(i) f(a) کی تعریف کی گئی ہے (ii) \(\lim\limits_{x \to a} f(x) \) موجود ہے (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
ذیل کے گراف میں پلاٹ کیے گئے فنکشنز کو چیک کریں۔ دونوں افعال تین تسلسل کی شرائط کو پورا نہیں کرتے ہیں:
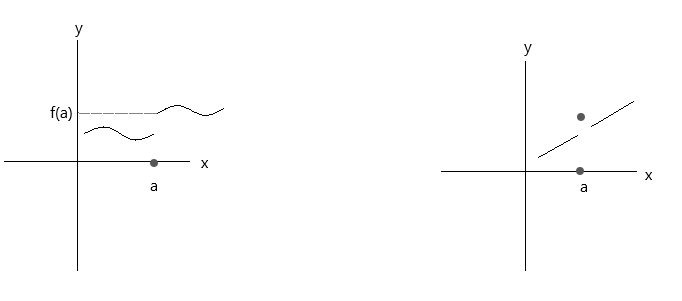
پہلے گراف کو دیکھیں، \(\lim\limits_{x \to a} f(x) \) = f(a) نقطہ a پر درست ہے اگر x دائیں جانب سے قدر 'a' تک پہنچتا ہے۔ لیکن اگر x بائیں جانب سے قدر 'a' تک پہنچتا ہے، f(x) f(a) کے قریب نہیں آرہا ہے، اس لیے یہ ایک منقطع فعل ہے۔