Hisoblashning ikkala qismi, Differensial va Integral hisoblar Limitlarga asoslanadi.
Limit nuqtaning eng yaxshi bashoratidir. Natijani to'g'ridan-to'g'ri hisoblay olmasak, bu bizga taxminiylikni beradi. Limit - bu funktsiyaning kirish ma'lum bir qiymatga "yaqinlashadigan" qiymati.
Keling, misol yordamida ushbu tushunchani tushunaylik.
f(x) = 4x − 3 bo‘lsin. f(x) ning qiymatlarini hisoblang, chunki x 3 ga yaqinroq qiymat oladi. f(x) = 4x − 3 funksiya grafigiga qarang. x 3 ga yaqinroq bo‘lgan nuqtalarni ko‘rib chiqing.
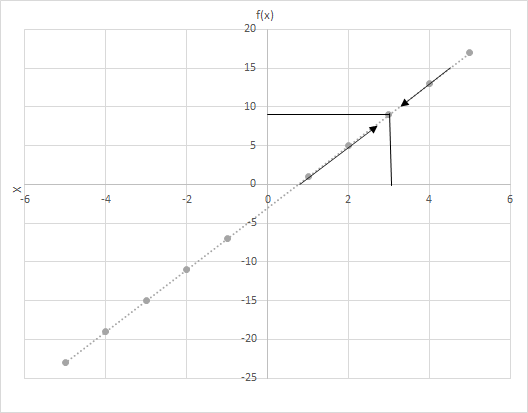
Bu erda ikkita stsenariyni ko'rib chiqing
(i) x chapdan 3 ga yaqinlashadi va
(ii) x o'ngdan 3 ga yaqinlashmoqda.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3,5 | 11 | |
| 2,5 | 7 | 3,2 | 9,8 | |
| 2,8 | 8,2 | 3,12 | 9,48 | |
| 2,9 | 8,6 | 3,1 | 9,4 | |
| 2,91 | 8,64 | 3,09 | 9,36 | |
| 2,95 | 8,8 | 3,05 | 9,2 | |
| 2,999 | 8,996 | 3.01 | 9.04 |
Oxirgi qatorni ko'ryapsizmi? Ikkala holatda ham x 3 ga yaqinlashganda, f(x) 9 ga yaqinlashadi. Shuning uchun biz quyidagilarni aytishimiz mumkin:
\(\lim\limits_{x \to 3} f(x) = 9\)
Yana bir misol keltiraylik, x 2 ga yaqinlashganda f(x) funksiyaning chegarasini toping, bu erda \(f(x) = \frac{x^2 - 4}{x-2}\) , ya'ni \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Agar x ning qiymatini 2 deb qo'ysak, biz quyidagilarga erishamiz: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{aniqlanmagan}\)
Bu ifodada x qiymatini o'rniga qo'yish orqali chegara qiymatini olish mumkin emasligini anglatadi. X 2 ga yaqinlashganda f(x) qiymatini hisoblaymiz.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,993 | . |
x 2 ga yaqinlashganda, \(f(x) = \frac{x^2 - 4}{x-2}\) qiymati 4 ga yaqinlashadi.
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Davomiylikni kontseptual jihatdan bir necha xil usullar bilan aniqlash mumkin. Funktsiya uzluksiz bo'ladi, agar uning grafigi qalamni sahifadan ko'tarmasdan qalam bilan kuzatilsa. Funktsiya uzluksiz bo'ladi, agar uning grafigi hech qanday teshiklari, bo'shliqlari va uzilishlari bo'lmagan buzilmagan egri chiziq bo'lsa. Quyidagi grafiklar uzluksiz funksiyalarni ifodalaydi.
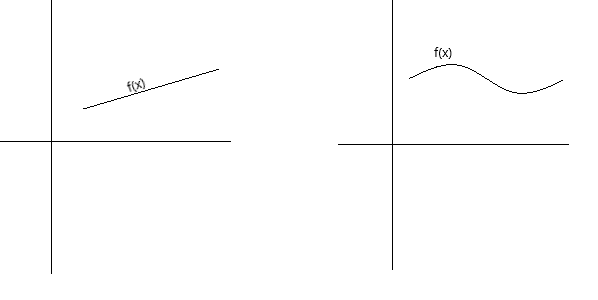
Uzluksizlikning yanada rasmiy ta'rifi sifatida f(x) funksiyani x = a nuqtada uzluksiz deb aytishimiz mumkin, agar quyidagi shartlar bajarilsa:
(i) f(a) aniqlanadi (ii) \(\lim\limits_{x \to a} f(x) \) mavjud (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Quyidagi grafiklarda tasvirlangan funktsiyalarni tekshiring. Ikkala funktsiya ham uchta uzluksizlik shartiga javob bermaydi:
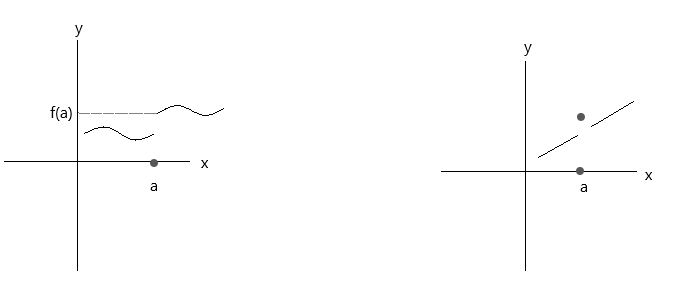
Birinchi grafaga qarang, a nuqtada \(\lim\limits_{x \to a} f(x) \) = f(a) to'g'ri bo'ladi, agar x "a" qiymatiga o'ng tomondan yaqinlashsa. Ammo agar x 'a' qiymatiga chap tomondan yaqinlashsa, f(x) f(a) ga yaqinlashmaydi, demak u uzluksiz funktsiyadir.