Cả hai phần của phép tính vi phân và tích phân đều dựa trên giới hạn .
Giới hạn là dự đoán tốt nhất của một điểm. Nó cung cấp cho chúng ta ước tính khi chúng ta không thể tính toán kết quả trực tiếp. Giới hạn là giá trị mà hàm 'tiến gần' khi đầu vào 'tiến gần' một giá trị nào đó.
Hãy cùng hiểu khái niệm này qua một ví dụ.
Cho f(x) = 4x − 3. Tính giá trị của f(x) khi x tiến gần hơn đến 3. Nhìn vào đồ thị của hàm số f(x) = 4x − 3. Kiểm tra các điểm tại đó x tiến gần hơn đến 3.
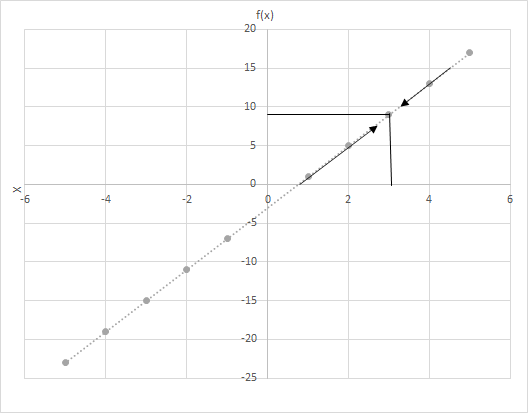
Hãy xem xét hai kịch bản ở đây
(i) x tiến tới 3 từ bên trái và
(ii) x tiến tới 3 từ bên phải.
| x | f(x) | x | f(x) | |
| 2 | 5 | 4 | 13 | |
| 2.2 | 5.8 | 3,5 | 11 | |
| 2,5 | 7 | 3.2 | 9.8 | |
| 2.8 | 8.2 | 3,12 | 9,48 | |
| 2,9 | 8,6 | 3.1 | 9.4 | |
| 2.91 | 8.64 | 3.09 | 9.36 | |
| 2.95 | 8.8 | 3.05 | 9.2 | |
| 2.999 | 8.996 | 3.01 | 9.04 |
Bạn có thấy hàng cuối cùng không? Trong cả hai trường hợp khi x tiến tới 3, f(x) tiến tới 9. Do đó, chúng ta có thể nói:
\(\lim\limits_{x \to 3} f(x) = 9\)
Hãy lấy một ví dụ khác, tìm giới hạn cho hàm số f(x) khi x tiến tới 2, trong đó \(f(x) = \frac{x^2 - 4}{x-2}\) , tức là \(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = ?\)
Nếu chúng ta đặt giá trị của x là 2, chúng ta sẽ có: \(\frac {(2^2- 4)} {(2 - 2)} =\frac{0}{ 0} = \textrm{không xác định}\)
Điều này ngụ ý rằng chúng ta không thể có được giá trị giới hạn bằng cách thay thế giá trị của x vào biểu thức. Hãy tính giá trị của f(x) khi x tiến tới 2.
| x | f(x) | x | f(x) |
| 1 | 3 | 2,5 | 4,5 |
| 1,2 | 3,2 | 2,2 | 4,2 |
| 1,5 | 3,5 | 2,1 | 4,1 |
| 1,8 | 3,8 | 2,05 | 4,05 |
| 1,9 | 3,9 | 2,01 | 4,01 |
| 1,99 | 3,99 |
Khi x tiến tới 2, giá trị của \(f(x) = \frac{x^2 - 4}{x-2}\) tiến tới 4. Do đó,
\(\lim\limits_{x \to 2} \frac{x^2-4}{x-2} = 4\)
Tính liên tục có thể được định nghĩa theo khái niệm theo một số cách khác nhau. Một hàm là liên tục nếu đồ thị của nó có thể được vẽ bằng bút mà không cần nhấc bút khỏi trang giấy. Một hàm là liên tục nếu đồ thị của nó là một đường cong không bị đứt đoạn, không có lỗ hổng, khoảng trống hoặc điểm gãy. Các đồ thị dưới đây biểu diễn các hàm liên tục.
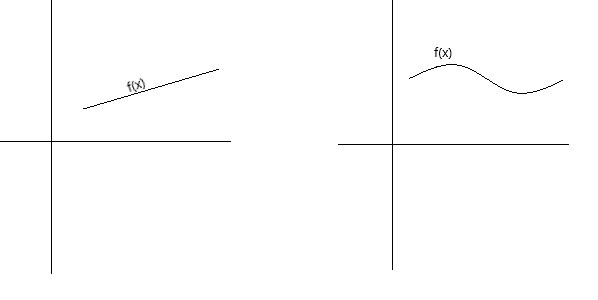
Theo định nghĩa chính thức hơn về tính liên tục, chúng ta có thể nói rằng hàm f(x) liên tục tại điểm x = a nếu các điều kiện sau được đáp ứng:
(i) f(a) được định nghĩa (ii) \(\lim\limits_{x \to a} f(x) \) tồn tại (iii) \(\lim\limits_{x \to a} f(x) \) = f(a)
Kiểm tra các hàm được vẽ trong đồ thị bên dưới. Cả hai hàm đều không thỏa mãn ba điều kiện liên tục:
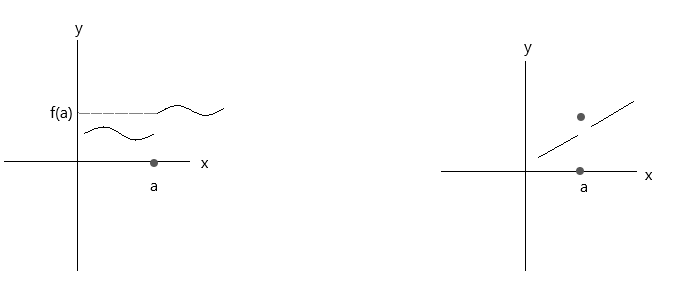
Hãy xem đồ thị đầu tiên, \(\lim\limits_{x \to a} f(x) \) = f(a) tại điểm a là đúng nếu x tiến tới giá trị 'a' từ phía bên phải. Nhưng nếu x tiến tới giá trị 'a' từ phía bên trái, f(x) không tiến tới f(a), do đó nó là một hàm không liên tục.