Back to the topics list

معادلات خطية

المعادلة الخطية هي معادلة للخط المستقيم. مثال: 2 س + ص = 5 معادلة خطية

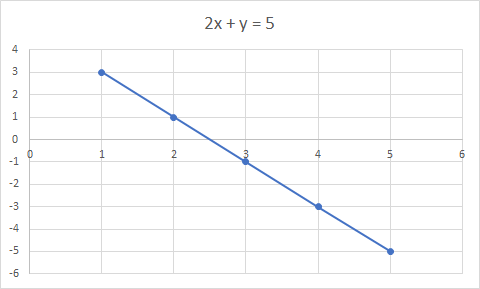
التمثيل البياني لـ 2x + y = 5 خط مستقيم

يمكننا تعريف المعادلة الخطية على النحو التالي:

المعادلة الخطية هي معادلة من الدرجة 1 وبالتالي تمثل خطًا مستقيمًا على الرسم البياني. تسمى المعادلات الخطية أيضًا كمعادلات من الدرجة الأولى ، حيث أن أعلى قوة للمتغير في هذه المعادلات هي 1.

كيف نقول إذا كانت المعادلة خطية أم لا؟ دعونا نفهم هذا مع بعض الأمثلة الواردة أدناه.

مثال:

• 2 س + 3 ص = 5

أي معادلة لها درجة. 2x + 3y = 5 له ثلاثة حدود. أعلى قوة للمتغير في المعادلة هي "الدرجة". هنا 2x ، x لديه قوة 1 أي x ¹ . في 3y ، y هي أيضًا ذات قوة 1 أي y ¹ ، وبالتالي فإن هذه المعادلة هي معادلة خطية

• 2 س + 3 ص + 5 س ص = 10

في هذه المعادلة ، درجة المصطلح 5xy هي اثنان. x للقوة 1 ، و y للقوة 1 ، وبالتالي فإن الدرجة الكلية ، وهي مجموع قوة كل متغيرات هذا المصطلح هي 1 + 1 = 2. لذلك ، هذه المعادلة ليست معادلة خطية.

• 2x + 3y + 7z + 9c = 20

في هذه المعادلة ، يوجد 5 حدود ولكن درجة كل هذه المصطلحات هي 1 ، وبالتالي فهذه معادلة خطية.

تعلمنا هنا أنه بالنسبة للمعادلة الخطية ، لا توجد قيود على عدد من المتغيرات في المعادلة. القيد على أعلى قوة يمكن أن يمتلكها مصطلح في المعادلة.

• \(\mathbf{\frac{2}{x} + y = 10}\)

في هذه المعادلة ، قوة x هي -1 (x ^-1 ) ، وبالتالي فإن هذه المعادلة ليست معادلة خطية.

حل المعادلات الخطية المتزامنة في متغيرين

يتم حل نظام من معادلتين ثابتتين ومستقلتين في متغيرين على النحو التالي:
يحل:
11 س - 7 ص = 13 …(أنا)
س - 7 ص = 3 ... (2)  

طريقة:

1. تخلص من أحد المجهول ( دعنا نحذف y) .
2. حل من أجل المجهول الآخر ( هنا هو x ).
3. أوجد قيمة المجهول المحذوف مسبقًا ( أوجد قيمة y )

للتخلص من أحد المجهول (الخطوة 1) ، يمكن استخدام الطرق التالية:

• طريقة الاستبدال
• طريقة الجمع أو الطرح

طريقة الاستبدال:
دعونا نحل المعادلات أعلاه باستخدام هذه الطريقة.
إلى عن على (أنا) نحصل على 11x - 7y = 13
−7y = 13-11x
\(y = \frac{(13 - 11x)}{-7} \)
عوض بقيمة y في المعادلة الثانية.
س - 7 ص = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
س + 13-11 س = 3
−10x = 3-13
−10x = −10
إذن ، x = 1
كـ \(y = \frac{(13 - 11x)}{-7} \) ، عوض بقيمة x هنا واحصل على قيمة y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
إذن ، x = 1 و y = −2 ∕ 7 هو الحل المطلوب.

طريقة القضاء:
يحل:
2 س + 3 ص = 10
س + ص = 6

1. اجعل معامل المتغير في كلتا المعادلتين هو نفسه (دعنا نقول y) بضرب كلتا المعادلتين في رقم.
   (2 س + 3 ص = 10) × 1
   (س + ص = 6) × 3
   كلتا المعادلتين لديها الآن معامل y كـ 3.
2. أضف أو اطرح للتخلص من متغير واحد ثم حل المعادلة بمتغير واحد متبقي (حل من أجل x)
   2 س + 3 ص = 10
   3 س + 3 ص = 18
   اطرح المعادلة الثانية من المعادلة الأولى.
   + 2 س + 3 ص = + 10
   + 3 س + 3 ص = +18
   - - -
   ------------------
   −x = -8
   إذن ، x = 8
   ص = 6 - س ⇒ ص = 6-8 = −2
   ومن ثم س = 8 ، ص = -2

مشاكل الكلمات التي تتضمن معادلات متزامنة:

مثال 1 : مجموع أرقام عدد معين مكون من رقمين هو 13 والرقم 2 أكثر من 7 أضعاف رقم الوحدة. أوجد الأرقام.
لنفترض أن x في خانة الوحدة و y في خانة العشرات.
10y + x = الرقم = yx
ص + س = 13
10 ص + س = 2 + 7 س ⇒ 10 ص - 6 س = 2
2 (5y −3x) = 2 ⇒ 5y - 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) ... باستخدام طريقة الاستبدال
ص + س = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3 س + 5 س = 13 × 5
1 + 8 س = 65 8 س = 64
س = 8 ، ص = 13 - س ⇒ ص = 13-8 = 5
العدد 10 × 5 + 8 = 58 (إجابة)

مثال 2: تبلغ تكلفة 3 علب قهوة وعبوتين شاي 15 دولارًا أمريكيًا وتكلفة علبة واحدة من علب القهوة و 4 علب شاي من نفس النوع هي 12 دولارًا أمريكيًا. ابحث عن تكلفة كل منها.
اجعل تكلفة علبة قهوة واحدة x دولارًا أمريكيًا ولعلبة شاي واحدة هي دولار y.
3 س + 2 ص = 16
1 س + 4 ص = 12
استخدم طريقة الاستبعاد ،
12 س + 8 ص = 64
+ 2 س + 8 ص = 24
- - -
----------------
10x = 40
س = 4 ، إذن 4 + 4 ص = 12 ص = 2
تبلغ تكلفة علبة واحدة من القهوة 4 دولارات ، وتبلغ تكلفة علبة الشاي 2 دولار. (إجابة)