Back to the topics list

xətti tənliklər

Xətti tənlik düz xətt üçün tənlikdir. Misal: 2x + y = 5 xətti tənlikdir

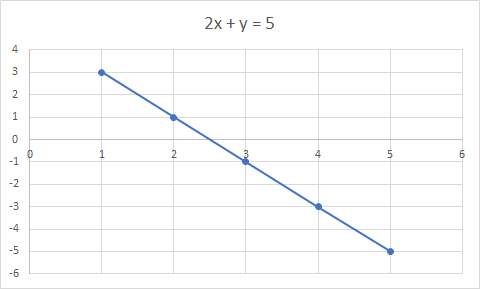
2x + y = 5 qrafiki düz xəttdir

Xətti tənliyi aşağıdakı kimi təyin edə bilərik:

Xətti tənlik 1 dərəcə tənliyidir və ona görə də qrafikdə düz xətti təmsil edir. Xətti tənliklərə birinci dərəcəli tənliklər də deyilir, çünki bu tənliklərdə dəyişənin ən yüksək gücü 1-dir.

Tənliyin xətti olub olmadığını necə deyə bilərik? Aşağıda verilmiş bir neçə nümunə ilə bunu anlayaq.

Misal:

• 2x + 3y = 5

İstənilən tənliyin dərəcəsi var. 2x +3y = 5-in üç üzvü var. Tənlikdəki dəyişənin ən yüksək gücü “dərəcə”dir. Burada 2x, x-in gücü 1, yəni x ¹ var. 3y-də y də 1 yəni y ¹ gücünə malikdir, ona görə də bu tənlik xətti tənlikdir.

• 2x + 3y + 5xy = 10

Bu tənlikdə 5xy termininin dərəcəsi ikidir. x 1-ci gücə, y isə 1-ə bərabərdir, ona görə də həmin terminin bütün dəyişənlərinin gücünün cəmi olan ümumi dərəcə 1 + 1 = 2-dir. Buna görə də bu tənlik xətti tənlik deyil .

• 2x + 3y + 7z + 9c = 20

Bu tənlikdə 5 hədd var, lakin bütün bu şərtlərin dərəcəsi 1-dir, ona görə də bu, xətti tənlikdir.

Burada öyrəndik ki, Xətti Tənlik üçün tənlikdə bir sıra dəyişənlər üçün heç bir məhdudiyyət yoxdur. Məhdudiyyət tənlikdəki bir terminin ola biləcəyi ən yüksək gücə aiddir.

• \(\mathbf{\frac{2}{x} + y = 10}\)

Bu tənlikdə x-in gücü -1 (x ^-1 ) olduğu üçün bu tənlik xətti tənlik deyil .

İki Dəyişəndə Sinxron Xətti Tənliklərin Həlli

İki dəyişənli iki ardıcıl və müstəqil tənlik sistemi aşağıdakı kimi həll olunur:
Həll edin:
11x − 7y = 13 …(i)
x − 7y = 3 …(ii)  

Metod:

1. Naməlumlardan birini aradan qaldırın ( gəlin y-ni aradan qaldıraq) .
2. Digər naməlumu həll edin ( burada x-dir ).
3. Daha əvvəl aradan qaldırılmış naməlumun qiymətini tapın ( y-nin dəyərini tapın)

Naməlumlardan birini aradan qaldırmaq üçün (addım 1) aşağıdakı üsullardan istifadə edilə bilər:

• Əvəzetmə üsulu
• Toplama və ya çıxma üsulu

Əvəzetmə üsulu:
Yuxarıdakı tənlikləri bu üsulla həll edək.
üçün (i) 11x − 7y = 13 alırıq
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
İkinci tənlikdə y-nin əvəzedici qiyməti.
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
Beləliklə, x = 1
\(y = \frac{(13 - 11x)}{-7} \) kimi, burada x-in qiymətini əvəz edin və y-nin qiymətini alın
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Deməli, x = 1 və y = −2 ∕ 7 tələb olunan həlldir.

Eliminasiya üsulu:
Həll edin:
2x + 3y = 10
x + y = 6

1. Hər iki tənliyi ədədə vuraraq dəyişənin əmsalını hər iki tənlikdə eyni edin (tutaq ki, y).
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   İndi hər iki tənliyin y əmsalı 3-ə bərabərdir.
2. Bir dəyişəndən xilas olmaq üçün əlavə və ya çıxın və sonra yalnız bir dəyişən qalan tənliyi həll edin (x üçün həll edin)
   2x + 3y = 10
   3x + 3y = 18
   Birinci tənlikdən ikinci tənliyi çıxarın.
   +2x + 3y =+10
   +3x + 3y = +18
   - - -
   ------------------
   −x = -8
   Beləliklə, x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   Beləliklə , x = 8, y = -2

Sinxron tənlikləri əhatə edən söz məsələləri:

Misal 1 : Müəyyən ikirəqəmli ədədin rəqəmlərinin cəmi 13-ə bərabərdir və ədəd vahidin rəqəmindən 7 dəfə çox 2-dir. Rəqəmləri tapın.
X vahid yerində, y isə onluq yerində olsun.
10y + x = ədəd=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … əvəzetmə metodundan istifadə etməklə
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, buna görə də y = 13 − x ⇒ y = 13 − 8 = 5
Rəqəm 10 × 5 + 8 = 58 (Cavab)

Misal 2: 3 qəhvə qabının və 2 çay paketinin qiyməti 15 dollar, bir qəhvə qabı və eyni tipli 4 çay paketinin qiyməti isə 12 dollardır. Hər birinin dəyərini tapın.
Bir qəhvə qabının qiyməti $x, bir çay paketinin qiyməti isə $y olsun.
3x + 2y = 16
1x + 4y = 12
aradan qaldırılması metodundan istifadə edin,
12x + 8y = 64
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4, buna görə də 4 + 4y = 12 ⇒ y = 2
Bir qəhvə qabının qiyməti 4 dollar, bir paket çayın qiyməti isə 2 dollardır.(Cavab)