Back to the topics list

রৈখিক সমীকরণ

একটি রৈখিক সমীকরণ একটি সরল রেখার জন্য একটি সমীকরণ। উদাহরণ: 2x + y = 5 একটি রৈখিক সমীকরণ

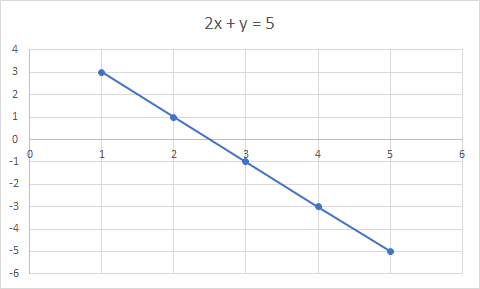
2x + y = 5 এর গ্রাফ একটি সরল রেখা

আমরা একটি রৈখিক সমীকরণকে এভাবে সংজ্ঞায়িত করতে পারি:

রৈখিক সমীকরণ হল ডিগ্রী 1 এর একটি সমীকরণ এবং তাই একটি গ্রাফে একটি সরল রেখার প্রতিনিধিত্ব করে। রৈখিক সমীকরণগুলিকে প্রথম ডিগ্রি সমীকরণও বলা হয়, কারণ এই সমীকরণগুলিতে চলকের সর্বোচ্চ শক্তি হল 1।

একটি সমীকরণ রৈখিক বা না হলে আমরা কিভাবে বলতে পারি? আসুন নীচে দেওয়া কয়েকটি উদাহরণ দিয়ে বিষয়টি বুঝতে পারি।

উদাহরণ:

• 2x + 3y = 5

যে কোনো সমীকরণের একটি ডিগ্রি আছে। 2x +3y = 5 এর তিনটি পদ আছে। একটি সমীকরণে চলকের সর্বোচ্চ শক্তি হল 'ডিগ্রী'। এখানে 2x, x এর একটি শক্তি 1 অর্থাৎ x ¹ । 3y-এ, yও 1 ক্ষমতার অর্থাৎ y ¹ , তাই এই সমীকরণটি একটি রৈখিক সমীকরণ

• 2x + 3y + 5xy = 10

এই সমীকরণে, 5xy শব্দটির ডিগ্রি দুটি। x এর শক্তি 1, এবং y হল 1 এর ক্ষমতা তাই মোট ডিগ্রী, যা সেই পদের সমস্ত ভেরিয়েবলের শক্তির সমষ্টি হল 1 + 1 = 2। অতএব, এই সমীকরণটি একটি রৈখিক সমীকরণ নয় ।

• 2x + 3y + 7z + 9c = 20

এই সমীকরণে, 5টি পদ রয়েছে কিন্তু এই সমস্ত পদের মাত্রা 1, তাই এটি একটি রৈখিক সমীকরণ।

এখানে আমরা শিখেছি যে একটি রৈখিক সমীকরণের জন্য সমীকরণের কয়েকটি চলকের উপর কোন সীমাবদ্ধতা নেই। একটি সমীকরণের একটি শব্দের সর্বোচ্চ শক্তির উপর সীমাবদ্ধতা রয়েছে।

• \(\mathbf{\frac{2}{x} + y = 10}\)

এই সমীকরণে, x এর শক্তি হল -1 (x ^-1 ), তাই এই সমীকরণটি একটি রৈখিক সমীকরণ নয় ।

দুটি ভেরিয়েবলে যুগপত রৈখিক সমীকরণ সমাধান করা

দুটি চলকের দুটি সামঞ্জস্যপূর্ণ এবং স্বাধীন সমীকরণের একটি সিস্টেম নিম্নরূপ সমাধান করা হয়:
সমাধান:
11x − 7y = 13 …(আমি)
x − 7y = 3 …(ii)  

পদ্ধতি:

1. অজানাগুলির একটিকে বাদ দিন ( চলুন y নির্মূল করি) ।
2. অন্যান্য অজানা জন্য সমাধান করুন ( এখানে এটি x )।
3. পূর্বে নির্মূল অজানা মান খুঁজুন ( y এর মান খুঁজুন )

একটি অজানা (ধাপ 1) দূর করতে নিম্নলিখিত পদ্ধতিগুলি ব্যবহার করা যেতে পারে:

• প্রতিস্থাপন পদ্ধতি
• যোগ বা বিয়োগ পদ্ধতি

প্রতিস্থাপন পদ্ধতি:
এই পদ্ধতি ব্যবহার করে উপরের সমীকরণগুলো সমাধান করা যাক।
জন্য (আমি) আমরা 11x − 7y = 13 পাই
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
দ্বিতীয় সমীকরণে y এর বিকল্প মান।
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
অতএব, x = 1
যেমন \(y = \frac{(13 - 11x)}{-7} \) , এখানে x এর মান প্রতিস্থাপন করুন এবং y এর মান পান
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
সুতরাং, x = 1 এবং y = −2 ∕ 7 হল প্রয়োজনীয় সমাধান।

নির্মূল পদ্ধতি:
সমাধান:
2x + 3y = 10
x + y = 6

1. একটি সংখ্যা দ্বারা উভয় সমীকরণ গুণ করে উভয় সমীকরণে একটি চলকের সহগকে একই করুন (যা বলা যাক y)।
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   উভয় সমীকরণের এখন 3 হিসাবে y সহগ রয়েছে।
2. একটি চলক থেকে পরিত্রাণ পেতে যোগ বা বিয়োগ করুন এবং তারপর শুধুমাত্র একটি চলক রেখে সমীকরণটি সমাধান করুন (x এর জন্য সমাধান করুন)
   2x + 3y = 10
   3x + 3y = 18
   প্রথম সমীকরণ থেকে দ্বিতীয় সমীকরণ বিয়োগ করুন।
   +2x + 3y =+10
   +3x + 3y = +18
   - - -
   ------------------
   −x = -8
   অতএব, x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   তাই x = 8, y = -2

যুগপত সমীকরণ জড়িত শব্দ সমস্যা:

উদাহরণ 1 : একটি নির্দিষ্ট দুই-অঙ্কের সংখ্যার অঙ্কের যোগফল হল 13 এবং সংখ্যাটি ইউনিটের অঙ্কের 7 গুণের বেশি। সংখ্যাগুলি সন্ধান করুন।
x একক স্থানে এবং y দশ স্থানে।
10y + x = সংখ্যা=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … প্রতিস্থাপন পদ্ধতি ব্যবহার করে
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, অতএব y = 13 − x ⇒ y = 13 − 8 = 5
সংখ্যাটি হল 10 × 5 + 8 = 58 (উত্তর)

উদাহরণ 2: 3 টি কফি টিন এবং 2 টি চায়ের প্যাকেটের দাম $15 এবং একটি কফি টিন এবং 4 টি চায়ের প্যাকেটের দাম $12। প্রতিটি খরচ খুঁজুন.
একটি কফি টিনের দাম $x এবং একটি চায়ের প্যাকেটের জন্য $y।
3x + 2y = 16
1x + 4y = 12
নির্মূল পদ্ধতি ব্যবহার করুন,
12x + 8y = 64
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4, অতএব 4 + 4y = 12 ⇒ y = 2
একটি কফি টিনের দাম $4 এবং একটি চায়ের প্যাকেটের দাম $2। (উত্তর)