Eine lineare Gleichung ist eine Gleichung für eine gerade Linie. Beispiel: 2x + y = 5 ist eine lineare Gleichung
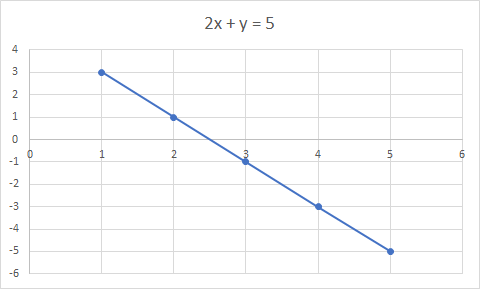
Der Graph von 2x + y = 5 ist eine gerade Linie
Wir können eine lineare Gleichung definieren als:
Eine lineare Gleichung ist eine Gleichung vom Grad 1 und stellt daher eine gerade Linie in einem Diagramm dar. Lineare Gleichungen werden auch als Gleichungen ersten Grades bezeichnet, da die höchste Potenz der Variablen in diesen Gleichungen 1 ist.
Wie sagt man, ob eine Gleichung linear ist oder nicht? Lassen Sie uns dies anhand einiger Beispiele unten verstehen.
Beispiel:
Jede Gleichung hat einen Grad. 2x +3y = 5 hat drei Terme. Die höchste Potenz der Variablen in einer Gleichung ist der „Grad“. Hier ist 2x, x hat eine Potenz von 1, dh x 1 . In 3y hat y auch die Potenz 1, dh y 1 , daher ist diese Gleichung eine lineare Gleichung
In dieser Gleichung ist der Grad des Terms 5xy zwei. x hat die Potenz 1 und y hat die Potenz 1, also ist der Gesamtgrad, der die Summe der Potenzen aller Variablen dieses Terms ist, 1 + 1 = 2. Daher ist diese Gleichung keine lineare Gleichung.
In dieser Gleichung gibt es 5 Terme, aber der Grad aller dieser Terme ist 1, daher ist dies eine lineare Gleichung.
Hier haben wir gelernt, dass es für eine lineare Gleichung keine Begrenzung der Anzahl von Variablen in der Gleichung gibt. Die Beschränkung liegt in der höchsten Potenz , die ein Term in einer Gleichung haben kann.
In dieser Gleichung ist die Potenz von x –1 (x –1 ), daher ist diese Gleichung keine lineare Gleichung.
Ein System aus zwei konsistenten und unabhängigen Gleichungen in zwei Variablen wird wie folgt gelöst:
Lösen:
11x − 7y = 13
x − 7y = 3
Methode:
Um eine der Unbekannten zu eliminieren (Schritt 1), können die folgenden Methoden verwendet werden:
Substitutionsmethode:
Lassen Sie uns die obigen Gleichungen mit dieser Methode lösen.
Zum
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Ersatzwert von y in der zweiten Gleichung.
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x = −10
Also x = 1
als \(y = \frac{(13 - 11x)}{-7} \) , ersetzen Sie den Wert von x hier und erhalten Sie den Wert von y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Also ist x = 1 und y = −2 ∕ 7 die gesuchte Lösung.
Eliminationsverfahren:
Lösen:
2x + 3y = 10
x + y = 6
Beispiel 1 : Die Summe der Ziffern einer bestimmten zweistelligen Zahl ist 13 und die Zahl ist 2 mehr als das 7-fache der Einerstelle. Finden Sie die Zahlen.
Sei x an der Einerstelle und y an der Zehnerstelle.
10y + x = die Zahl=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … unter Verwendung der Substitutionsmethode
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, also y = 13 − x ⇒ y = 13 − 8 = 5
Die Zahl ist 10 × 5 + 8 = 58 (Antwort)
Beispiel 2: 3 Kaffeedosen und 2 Teepäckchen kosten 15 €, eine Kaffeedose und 4 Teepäckchen der gleichen Sorte 12 €. Finden Sie die Kosten für jeden.
Angenommen, die Kosten für eine Kaffeedose betragen x $ und für eine Teepackung y $.
3x + 2y = 16
1x + 4y = 12
Verwenden Sie die Eliminierungsmethode,
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4, also 4 + 4y = 12 ⇒ y = 2
Die Kosten für eine Kaffeedose betragen 4 $ und die Kosten für ein Teepaket 2 $. (Antwort)