Una ecuación lineal es una ecuación para una línea recta. Ejemplo: 2x + y = 5 es una ecuación lineal
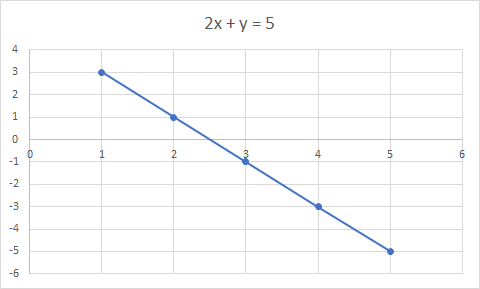
La gráfica de 2x + y = 5 es una línea recta
Podemos definir una Ecuación Lineal como:
La ecuación lineal es una ecuación de grado 1 y, por lo tanto, representa una línea recta en un gráfico. Las ecuaciones lineales también se denominan ecuaciones de primer grado , ya que la potencia más alta de la variable en estas ecuaciones es 1.
¿Cómo decimos si una ecuación es lineal o no? Entendamos esto con algunos ejemplos dados a continuación.
Ejemplo:
Cualquier ecuación tiene un grado. 2x +3y = 5 tiene tres términos. La potencia más alta de la variable en una ecuación es el 'grado'. Aquí está 2x, x tiene una potencia de 1, es decir, x 1 . En 3y, y también es de potencia 1, es decir, y 1 , por lo tanto, esta ecuación es una ecuación lineal
En esta ecuación, el grado del término 5xy es dos. x es de potencia 1 e y es de potencia 1 por lo que el grado total, que es la suma de la potencia de todas las variables de ese término es 1 + 1 = 2. Por lo tanto, esta ecuación no es una ecuación lineal.
En esta ecuación, hay 5 términos pero el grado de todos estos términos es 1, por lo tanto, esta es una ecuación lineal.
Aquí aprendimos que para una ecuación lineal no hay limitación en un número de variables en la ecuación. La limitación está en la potencia más alta que puede tener un término en una ecuación.
En esta ecuación, la potencia de x es -1 (x -1 ), por lo tanto, esta ecuación no es una ecuación lineal.
Un sistema de dos ecuaciones consistentes e independientes en dos variables se resuelve de la siguiente manera:
Resolver:
11x − 7y = 13
x − 7y = 3
Método:
Para eliminar uno de los desconocidos (paso 1), se pueden utilizar los siguientes métodos:
Método de sustitución:
Resolvamos las ecuaciones anteriores usando este método.
Para
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Sustituye el valor de y en la segunda ecuación.
x - 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
Por lo tanto, x = 1
como \(y = \frac{(13 - 11x)}{-7} \) , sustituya el valor de x aquí y obtenga el valor de y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Por lo tanto, x = 1 y y = −2 ∕ 7 es la solución requerida.
Método de eliminación:
Resolver:
2x + 3y = 10
x + y = 6
Ejemplo 1 : La suma de los dígitos de cierto número de dos dígitos es 13 y el número es 2 más que 7 veces el dígito de la unidad. Encuentra los números.
Sea x en el lugar de la unidad e y en el lugar de las decenas.
10y + x = el numero=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … usando el método de sustitución
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, por lo tanto y = 13 − x ⇒ y = 13 − 8 = 5
El número es 10 × 5 + 8 = 58 (Respuesta)
Ejemplo 2: El costo de 3 latas de café y 2 paquetes de té es de $15 y el de una lata de café y 4 paquetes de té del mismo tipo es de $12. Encuentre el costo de cada uno.
Supongamos que el costo de una lata de café es $x y el de un paquete de té es $y.
3x + 2y = 16
1x + 4y = 12
Utilice el método de eliminación,
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4, por lo tanto 4 + 4y = 12 ⇒ y = 2
El costo de una lata de café es de $4 y el costo de un paquete de té es de $2. (Respuesta)